I come from an optimization background and ventured into probabilistic programming pretty recently.
I’m trying to use (num)pyro to model a stochastic generative function to generate DVRP synthetic instances. One heavy assumption I’m going with is that DVRP problems have an underlying stochastic nature (for example a particular city might have the same underlying spatiotemporal randomness in service requests day after day).
Below I have a sort of generative code that kind of does along the lines of what I want but I want to have a much more generalized model than can also do inference and fit other actual data.
def model():
# 1. sample number of rectangular regions
nRegions = numpyro.sample("nRegions", dist.DiscreteUniform(30, 35))
region_list = []
# 2. for each region sample the size and temporal charateristics
for region in range(nRegions):
w = numpyro.sample("width_{}".format(region), dist.DiscreteUniform(4, 20))
h = numpyro.sample("height_{}".format(region), dist.DiscreteUniform(4, 20))
# x and y are the bottom left corner of the rectangle
x = numpyro.sample("x_{}".format(region), dist.DiscreteUniform(0, GRID-w))
y = numpyro.sample("y_{}".format(region), dist.DiscreteUniform(0, GRID-h))
# temporal characteristics (with atmost one peak for now)
local_mu = numpyro.sample("mu_{}".format(region), dist.Uniform(0, TIME_STEPS))
local_sigma = numpyro.sample("sigma_{}".format(region), dist.Uniform(0, TIME_STEPS//8))
# sample rates for each region from a uniform distribution
local_rate = numpyro.sample("local_probs_{}".format(region), dist.Uniform(0, 1))
region_list.append((x, y, w, h, local_rate, (local_mu, local_sigma)))
return region_list
def sample_events(region_list):
BASE_RANDOMNESS = 1 / 100 # 0.1% of the whole grid should have a base randomness
events = []
for x, y, w, h, local_rate, (local_mu, local_sigma) in region_list:
for i in range(x, x+w):
for j in range(y, y+h):
# sample number of events from a poisson distribution with the local rate
num_events = numpyro.sample("_", dist.Poisson(local_rate))
for _ in range(num_events):
# sample the time of the event from a normal distribution with the local mu and sigma
time = numpyro.sample("_", dist.Normal(local_mu, local_sigma))
events.append((i, j, time))
# sample a bunch of random events from all over the grid with a base poisson rate
return events
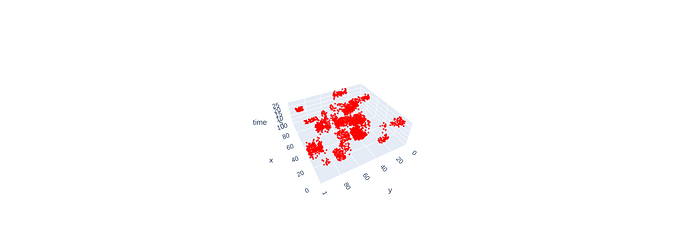
Below is one realization of the above code (plotted with plotly)
The above code basically defines a number of rectangular regions in a discrete grid, and each region has its own temporal signature (a 1D gaussian) and a poission rate. For each point in the grid I then sample a number of events (preferably 0 or 1 or almost 2) with a poison rate given by the generative code. Then for each event I sample the timesteps it can occur with the point’s temporal signature.
I’m wondering if there is a better way to model this situation that also makes it easy for inference.
Another idea I’ve tried is that defining a 3d gaussian mixture with n components and calculate the pdf at each grid point and scale the values to be between 0 and 1 so that it parameterized a Bernoulli on each of the grid points (a 3d lattice). The problem with this is when I sample from this Bernoulli grid, it kind of assumes that the same point in space is independent which leads to the same point generating a service request at different points in time, which doesn’t make much sense.
Feel free to ask any questions or details I may have left out.
EDIT 1 :- For context the output of the stochastic model (an instance of DVRP) can be something like List[(x_coord :int, y_coord :int, time :float or int)]. These are also the observed variables when I do inference on different datasets of similar instances.