Model with a discrete deterministic step: MCMC works, but SVI fails

Misc.
1

Setup

Hi everyone,

I’ve been trying to build a model with a continuous latent variable that goes through a discrete deterministic step before being observed. In this case, the continous latent variable gets rounded to the nearest integer. Here is a simple toy model :

def model(n_data_points=1, data=None):
    continuous = pyro.sample("continuous", dist.Uniform(0, 10))
    discrete = pyro.deterministic("discrete", torch.round(continuous))
    with pyro.plate("data_points", n_data_points):
        return pyro.sample("observed", dist.Normal(loc=discrete, scale=1), obs=data)

Let’s say the true value of the latent variable is around 8. I generate 100 observed data points that match this assumption:

data = torch.randn((100,)) + 8

Using MCMC: works as expected

Using MCMC to sample the posterior gives the expected results:

pyro.clear_param_store()

from pyro.infer.mcmc.api import MCMC
from pyro.infer.mcmc import NUTS
pyro.set_rng_seed(2)
kernel = NUTS(model)
mcmc = MCMC(kernel, num_samples=100, warmup_steps=50)
mcmc.run(n_data_points=len(data), data=data)
mcmc.summary()

Output:


                  mean       std    median      5.0%     95.0%     n_eff     r_hat
  continuous      8.06      0.30      8.07      7.56      8.43     67.28      0.99

Number of divergences: 31

So far, so good.

However, I noticed that the sampling was particularly slow compared to other models I have tried.

Using SVI: Does not converge

Here is my attempt at using SVI:

pyro.clear_param_store()

guide = pyro.infer.autoguide.AutoDiagonalNormal(model)

adam = pyro.optim.Adam({"lr": 0.001})
elbo = pyro.infer.Trace_ELBO(num_particles=1)
svi = pyro.infer.SVI(model, guide, adam, elbo)

for step in range(5000):
    loss = svi.step(n_data_points=len(data), data=data)

The elbo loss does not go down but seems to move around randomly.

svi

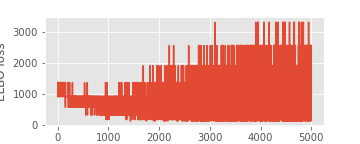
What I’ve tried

  • Using AutoDelta to perform MAP estimation instead of AutoDiagonalNormal: behavior is similar.
  • Increasing or decreasing the learning rate by powers of 10: behavior is similar, although with bigger learning rates, the loss even tends to increase over time.
  • Increasing num_particles in ELBO loss to try to stabilize the loss: behavior stays the same.
  • Using TraceGraph_ELBO instead of Trace_ELBO.

Is there a problem with how I wrote my model and inference routine? I’m new to Pyro so I could have missed something obvious here.

2

the discontinuity (non-differentiability) introduced by round is a problem. actually for both methods but more severe for svi. the mcmc will use metropolis-hasting corrections that correct for the fact that the target surface is not differentiable.

i’d suggest you give discrete a prior distribution that is actually discrete (e.g. Categorical). strange mixes of continuous and discrete will probably just give you lots of problems

3

Thanks for the answer! I actually started using this method because I could not figure out how to infer the posterior distribution of the discrete latent variable. I’ll try to go back to modeling it directly as a categorical variable.