I am using dist.Dirichlet() to model probabilities but when looking at the retrodictions after fitting they are not as I expect. I suspect I am doing something fundamentally wrong. Here is a simple example with 5 groups where the first column has very low probability and last column has high.
import numpy as np
import jax
import jax.numpy as jnp
import jax.random as random
import numpyro
from numpyro import distributions as dist
from numpyro.infer import NUTS, MCMC, Predictive
import arviz as az
numpyro.set_host_device_count(1)
N_ = 100
X = jax.nn.softmax(np.random.normal(np.arange(-4, 4.1, step=2), scale=2., size=(N_, 5)), axis=-1)
def model1(X=None):
with numpyro.plate('plate_people', 5):
a = numpyro.sample('a', dist.Normal(0, 5.))
b = numpyro.deterministic('b', jax.nn.softplus(a))
obs = numpyro.sample('obs', dist.Dirichlet(b), obs=X)
hmc = MCMC(NUTS(model1, target_accept_prob=0.9, ), num_chains=4, num_warmup=1000, num_samples=1000, progress_bar=True, chain_method='sequential')
hmc.run(random.PRNGKey(32), X=X)
ppc = Predictive(model1, hmc.get_samples())(random.PRNGKey(48), )
idata = az.from_numpyro(hmc, posterior_predictive=ppc)
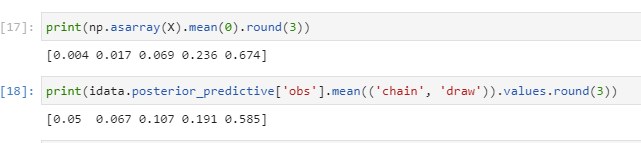
print(np.asarray(X).mean(0).round(3))
print(idata.posterior_predictive['obs'].mean(('chain', 'draw')).values.round(3))
Looking just at the first column, in the data X both the mean and 90th percentile are less than 0.005.
But in the predictions mean is 0.05 and 90th percentile is 0.15
How can I capture this in the model? I’ve tried increasing the number of rows (N) but it doesn’t have any impact.
I think the result implies that Dirichlet might not be the likelihood that you need. You can perform maximum likelihood to find which Dirichlet distribution best for generating your data:
from numpyro.infer import SVI, Trace_ELBO
def model(X=None):
a = numpyro.param('a', jnp.ones(5), constraint=dist.constraints.positive)
obs = numpyro.sample('obs', dist.Dirichlet(a), obs=X)
guide = lambda *args, **kwargs: None
svi = SVI(model, guide, numpyro.optim.Adam(0.1), Trace_ELBO())
svi_result = svi.run(random.PRNGKey(0), 1000, X)
dist.Dirichlet(svi_result.params['a']).mean
I think the result will agree with MCMC result. If you generate data X using a Dirichlet distribution, then SVI & MCMC should recover that process.
Edit: The generative process of your data is SoftmaxNormal, not Dirichlet. I think what we get is the mean of the best Dirichlet approximation of your SoftmaxNormal is different from the mean of the SoftmaxNormal.
1 Like
Ok noted, thanks for checking. I am not tied to the Dirichlet distribution. Is there another approach I can use within MCMC? I see that there isn’t a SoftMax transform.
Currently, we don’t have inference methods for non-invertible-transformed observations like the ones come from jax.nn.softmax. I’m not sure how to derive an analytic formula for Softmax-Normal likelihood. The closest distribution that I found is Multivariate Logit-normal distribution.
I saw that there was a SoftMax bijector in tfp and played around a bit but couldn’t get any decent models with it.
For now I’ll revert to modelling the probabilities individually so that within each observation row they don’t sum to 1.
Thanks for the help anyway
Yes, TFP has softmax centered transform, which is the one used in Multivariate Logit-normal distribution in my last comment. It is a bit different from softmax.
