Model explodes and goes up in flames - Exploding Gradients?

Misc.
1

Hi everyone!

I’m trying to build a simple Bayesian Regression Model in Pyro - however, when starting the SVI, the AutoDiagonalGuide immediately throws an error (see message below) and the custom guide I wrote sometimes crashes too, sometimes works. The error is caused by guide parameters becoming undefined (NaN), I assume due to exploding gradients? I’m still fairly new to Pyro and Bayesian Statistics in general, so it’s probably just some really stupid mistake on my side. Also, I was wondering: In this setup, I don’t learn the posterior for z, but directly learn the parameters for w instead - is this a problem? Although the ELBO loss decreases, it is usually still super high (e^10), even after thousands of svi steps. I’m just really confused right now, I can’t get it to work.
Thank you for reading and thank you even more for replying!

Here is the model in question:
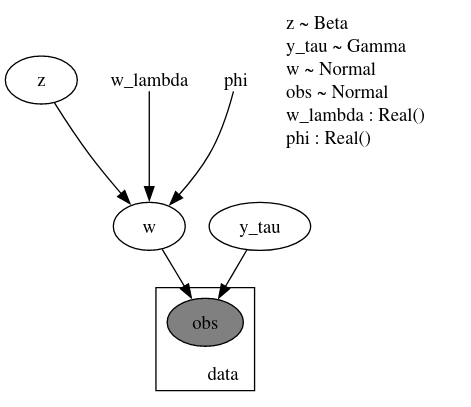
grafik

And here is the guide:
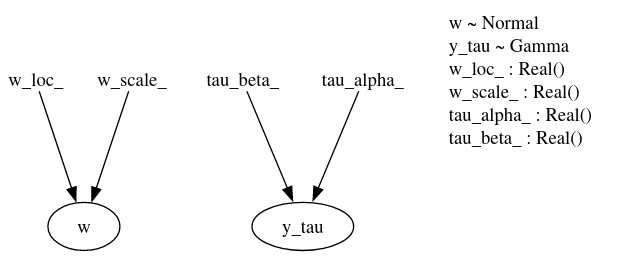
grafik

Error Message from AutoDiagonalNormal Guide

ValueError: Expected parameter loc (Parameter of shape (1001,)) of distribution Normal(loc: torch.Size([1001]), scale: torch.Size([1001])) to satisfy the constraint Real(), but found invalid values:
Parameter containing:
tensor([-0.5683, -1.5561, -0.1919, …, 0.0349, -0.0553, 0.1487],
requires_grad=True)
Trace Shapes:
Param Sites:
AutoDiagonalNormal.loc 1001
AutoDiagonalNormal.scale 1001
Sample Sites:

2

Hi @Bjarne, I think you can print out some parameter values and inspect the model directly. It is hard to guess where things go wrong.

3

Hi @fehiepsi, thanks for your reply. I inspected some of the model parameters directly and confirmed that there are NaN values in AutoDiagonalNormal.loc, or tau_beta_ respectively. Are there other parameters that would be interesting to inspect in that case? I thought, there might be something wrong with my model/guide setup in general. Best regards!

4

you don’t need to look at the place NaN happens. you can use some initial values and try to see why elbo is large via computing log probability of each variable in your model explicitly. log probability can be computed via distribution.log_prob(value)