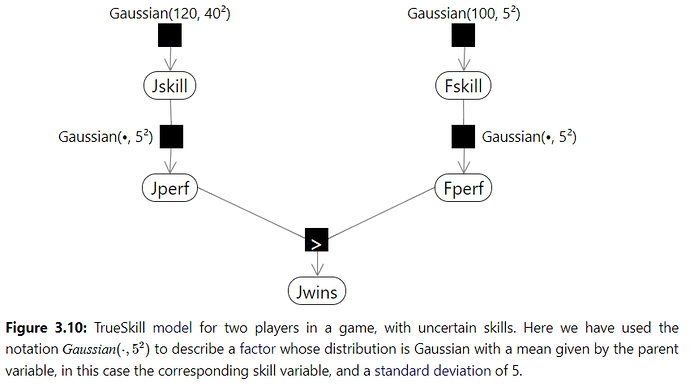
Hi, I am working on Chapter 3, on the following model:
We sample Jill skills from a Gaussian distribution, and we use that sampled value to sample performance form N(Jillskill, 5). We do the same for Fred. We have a deterministic factor checking if Jill wins. We expect that if Fred wins twice, his skill is believed to be higher.
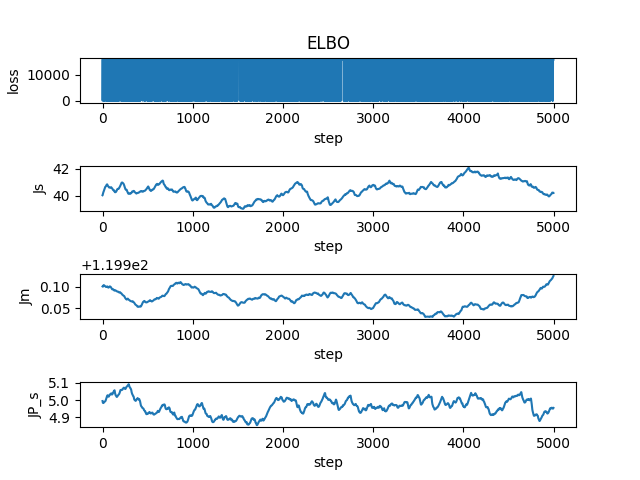
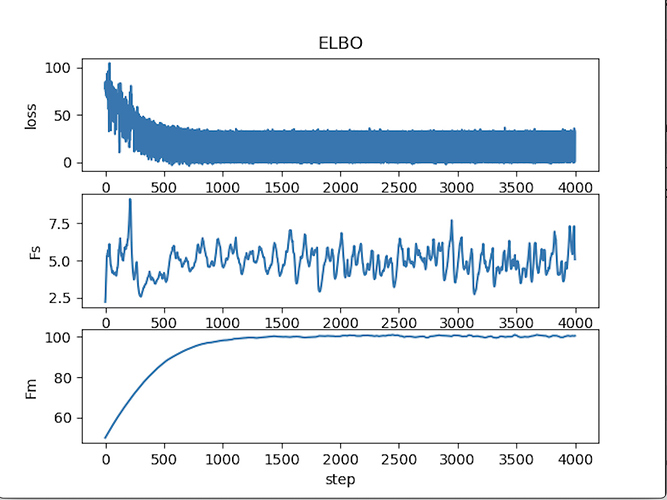
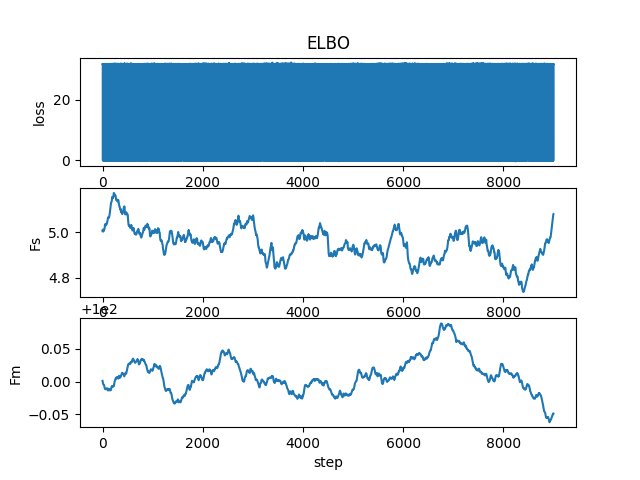
I plot the loss and it is just oscillating, see the plot below. Fm and Fs are the mean and standard deviation of Fred with input [0,0] (Jill lost twice)
Here is the code, can you help me find where is the problem?
import matplotlib.pyplot as plt
import numpy as np
import torch
import pyro
import pyro.distributions as dist
import pyro.infer
import pyro.optim
from pyro.optim import Adam
import torch.distributions.constraints as constraints
def scale(Data):
Jskill = pyro.sample('JS', dist.Normal(120.,40.))
Jperf = pyro.sample('JP', dist.Normal(Jskill, 5.))
Fskill = pyro.sample('FS', dist.Normal(100.,5.))
Fperf = pyro.sample('FP', dist.Normal(Fskill, 5.))
Jwin = torch.tensor([0.0])
if Fperf<Jperf:
Jwin = torch.tensor([1.0])
with pyro.plate("plate", len(Data)):
a= pyro.sample('JW', dist.Bernoulli(Jwin), obs=Data)
def guide(Data):
J_m = pyro.param('J_m', torch.tensor(120.0))
J_s = pyro.param('J_s', torch.tensor(40.0), constraint = constraints.positive)
F_m = pyro.param('F_m', torch.tensor(100.0))
F_s = pyro.param('F_s', torch.tensor(5.0), constraint=constraints.positive)
Jp_s = pyro.param('JP_s', torch.tensor(5.0), constraint=constraints.positive)
Fp_s = pyro.param('FP_s', torch.tensor(5.0),constraint=constraints.positive)
Jskill = pyro.sample('JS', dist.Normal(J_m,J_s))
Jperf = pyro.sample('JP', dist.Normal(Jskill, Jp_s))
Fskill = pyro.sample('FS', dist.Normal(F_m,F_s))
Fperf = pyro.sample('FP', dist.Normal(Fskill,Fp_s))
Data = torch.tensor([0.0, 0.0]) # Jill loses twice
pyro.clear_param_store()
adam_params = {"lr": 0.001, "betas": (.9, .999)}
optimizer = Adam(adam_params)
svi = pyro.infer.SVI(model=scale,
guide=guide,
optim=optimizer,
loss=pyro.infer.Trace_ELBO())
losses, a,b = [], [], []
num_steps = 9000
for t in range(num_steps):
losses.append(svi.step(Data))
a.append(pyro.param("F_s").item())
b.append(pyro.param("F_m").item())
plt.subplot(3,1,1)
plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
plt.subplot(3,1,2)
plt.plot(a)
plt.xlabel('step')
plt.ylabel('Fs')
plt.subplot(3,1,3)
plt.plot(b)
plt.xlabel('step')
plt.ylabel('Fm')
plt.savefig('Floss.png')
print('FS = ',pyro.param("F_s").item())
print('FP = ', pyro.param("F_m").item())