MLE for Normal distribution parameters

Misc.
1

Hi,
I’m trying a very simple exercise in Pyro – to learn the parameters of a univariate normal distribution via MLE. I’m doing this for purely learning purposes. While the MLE is trivial (dataset mean and dataset variance), I am trying to do the same using autograd. I see that there are examples on estimating the full Bayesian via SVI, however, I am unaware of examples on the trivial MLE.

import pyro
import pyro.distributions as dist

uv_normal = dist.Normal(loc=1., scale=1.)
train_data = uv_normal.sample([10000])

Once I have the samples, I create a loc parameter.

pyro.clear_param_store()
loc = pyro.param("loc", init_tensor=torch.tensor(0.1))

and then use simple gradient descent where I compute the gradient of the negative log likelihood (-torch.mean(to_train.log_prob(train_data)) to update loc.

for i in range(10):
    to_train = dist.Normal(loc=loc, scale=1.0)
    loss = -torch.mean(to_train.log_prob(train_data))
    
    loss.backward()
    print(to_train, loss, loc, loc.grad)
    loc = loc - 0.00001*loc.grad

However, I get the output and the error below:

Normal(loc: 0.10000000149011612, scale: 1.0) tensor(1.4146, grad_fn=<NegBackward0>) tensor(0.1000, requires_grad=True) tensor(0.0800)
Normal(loc: 0.09999920427799225, scale: 1.0) tensor(1.4146, grad_fn=<NegBackward0>) tensor(0.1000, grad_fn=<SubBackward0>) None

TypeError                                 Traceback (most recent call last)
Input In [99], in <module>
      7 loss.backward()
      8 print(to_train, loss, loc, loc.grad)
----> 9 loc = loc - 0.00001*loc.grad

TypeError: unsupported operand type(s) for *: 'float' and 'NoneType'

Clearly, the gradient becomes None.

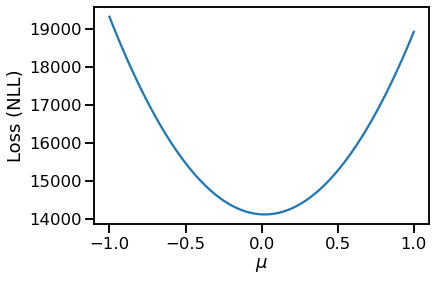
Ofcourse, if I visually inspect the loss (NLL) for a discrete set of locs, I get the expected plot:

losses = {}
for i in torch.linspace(-1.0, 1.0, 100):
    losses[i.item()] = -torch.sum(dist.Normal(loc=i, scale=1.0).log_prob(train_data)).item()

import pandas as pd
pd.Series(losses).plot(xlabel=r"$\mu$", ylabel="Loss (NLL)")

loss-pyro

However, I was able to use pretty much the same code as above in TF Probability as follows to learn the MLE for loc.

Working TensorFlow Probability code for the same problem

import tensorflow as tf
import tensorflow_probability as tfp

uv_normal = tfd.Normal(loc=0., scale=1.)
train_data = uv_normal.sample(10000)
to_train = tfd.Normal(loc = tf.Variable(-1., name='loc'), scale = 1.)

def nll(train):
    return -tf.reduce_mean(to_train.log_prob(train))

def get_loss_and_grads(train):
    with tf.GradientTape() as tape:
        tape.watch(to_train.trainable_variables)
        loss = nll(train)
    grads = tape.gradient(loss, to_train.trainable_variables)
    return loss, grads

optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)

iterations = 500
losses = np.empty(iterations)
vals = np.empty(iterations)
for i in range(iterations):
    loss, grads = get_loss_and_grads(train_data)
    losses[i] = loss
    vals[i] = to_train.trainable_variables[0].numpy()
    optimizer.apply_gradients(zip(grads, to_train.trainable_variables))
    if i%50 == 0:
        print(i, loss.numpy())

After the 500 iterations, I am able to learn the correct loc in TFP.

  1. I wanted to check if I am making a mistake or missing something obvious. Or, in short, what would be the best way to compute the MLE for the above problem for estimating the parameters of the distribution?
  2. What would be an efficient way to write the following code:
for i in torch.linspace(-1.0, 1.0, 100):
    losses[i.item()] = -torch.sum(dist.Normal(loc=i, scale=1.0).log_prob(train_data)).item()

If I’m able to get this to work, I’d be happy to make PRs to the documentation and add examples on MLE, MAP, and Full Bayesian (via SVI). As an example, I created a post on Coin tosses: MLE, MAP and Full Bayesian using TFP. I’d like to be able to get it working on Pyro.

2

the code you’ve written isn’t using parameters correctly. you can’t hack together a custom optimization loop the way you’ve done.

1 Like
3

Thanks, @martinjankowiak
I was trying to not use SVI for MLE as it seemed like an overkill. I wanted to share a working version for MLE estimate for loc and scale (currently using PyTorch distributions). Complete blog post containing full code.

Here is the minimal code for learning loc given fixed scale. In a previous version of the code, I missed the zero_grad().

learning loc given fixed scale 

import torch
dist = torch.distributions
uv_normal = dist.Normal(loc=0.0, scale=1.0)
train_data = uv_normal.sample([10000])
loc = torch.autograd.Variable(torch.tensor(-10.0), requires_grad=True)
opt = torch.optim.Adam([loc], lr=0.01)
for i in range(3100):
    to_learn = torch.distributions.Normal(loc=loc, scale=1.0)
    loss = -torch.sum(to_learn.log_prob(train_data))
    loss.backward()
    if i % 500 == 0:
        print(f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc.item():0.2f}")
    opt.step()
    opt.zero_grad()

This gives the learnt loc same as analytical MLE solution (train_data.mean())

learning loc and scale

The important difference here was that I introduced softplus to ensure positivity of scale.

loc = torch.autograd.Variable(torch.tensor(-10.0), requires_grad=True)
scale = torch.autograd.Variable(torch.tensor(2.0), requires_grad=True)

opt = torch.optim.Adam([loc, scale], lr=0.01)
for i in range(5100):
    scale_softplus = torch.functional.F.softplus(scale)

    to_learn = torch.distributions.Normal(loc=loc, scale=scale_softplus)
    loss = -torch.sum(to_learn.log_prob(train_data))
    loss.backward()
    if i % 500 == 0:
        print(
            f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc.item():0.2f}, Scale: {scale_softplus.item():0.2f}"
        )
    opt.step()
    opt.zero_grad()

I’m able to get the correct loc and scale.

  1. Would using a uniform prior and no guide and then use SVI be the MLE?
  2. Following up on the previous, will setting our non-uniform prior and no guide and SVI be equivalent to the MAP solution?

If the answer to the above is yes for both, would it be helpful to include sample code such as mine for MLE and MAP instead of running SVI?