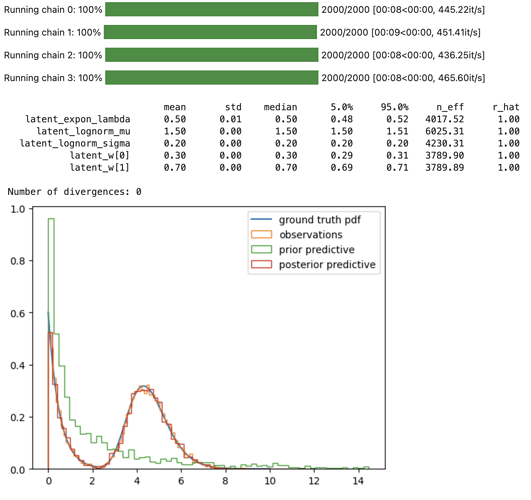
Hi!
I see there’s the MixtureSameFamily class both in pyro and numpyro, whereas numpyro additionally has MixtureGeneral. Is this difference due to some underlying limitation of pyro vis-a-vis numpyro? How should I go about achieving some equivalent of MixtureGeneral in pyro? Below is a toy example of a model in numpyro that I’m curious how to do in pyro as well. Thanks!
import numpy as np
from scipy.stats import expon, lognorm, bernoulli
from matplotlib import pyplot as plt
from jax import random
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
import numpyro.handlers as handl
from numpyro.infer import MCMC, NUTS, SVI, Predictive, Trace_ELBO, autoguide
numpyro.util.set_host_device_count(4)
rng_key = random.PRNGKey(0)
rng = np.random.default_rng(0)
# DATA GENERATION
## ground truth
w = 0.3
expon_lambda = 0.5
lognorm_mu = 1.5
lognorm_sigma = 0.2
## pdf
x = np.linspace(0, 10, 1_000)
y = w * expon(scale=expon_lambda).pdf(x) + (1 - w) * lognorm(scale=np.exp(lognorm_mu), s=lognorm_sigma).pdf(x)
## rvs
N = 10_000
_w = bernoulli(p=w).rvs(size=N, random_state=rng)
expon_rvs = expon(scale=expon_lambda).rvs(size=N, random_state=rng)
lognorm_rvs = lognorm(scale=np.exp(lognorm_mu), s=lognorm_sigma).rvs(size=N, random_state=rng)
rvs = _w * expon_rvs + (1 - _w) * lognorm_rvs
# MODEL
def model(n_obs):
latent_expon_lambda = numpyro.sample("latent_expon_lambda", dist.TruncatedNormal(loc=0, scale=1.0, low=0, high=3.0))
latent_lognorm_mu = numpyro.sample("latent_lognorm_mu", dist.Normal(loc=1, scale=1.0))
latent_lognorm_sigma = numpyro.sample("latent_lognorm_sigma", dist.HalfNormal(scale=1.0))
latent_w = numpyro.sample("latent_w", dist.Dirichlet(concentration=jnp.array([1.0, 1.0])))
component_dists = [
dist.Exponential(rate=1/latent_expon_lambda),
dist.LogNormal(loc=latent_lognorm_mu, scale=latent_lognorm_sigma),
]
with numpyro.plate("obs_plate", n_obs):
obs = numpyro.sample(
"obs",
dist.MixtureGeneral(
mixing_distribution=dist.Categorical(probs=latent_w),
component_distributions=component_dists))
# PRIOR PREDICTIVE
rng_key, rng_key_ = random.split(rng_key)
prior_pred = Predictive(model, num_samples=2_000)(rng_key_, n_obs=1)
_prior_obs = prior_pred["obs"].reshape(-1)
prior_obs = _prior_obs[_prior_obs < np.percentile(_prior_obs, 95)]
# MCMC
mcmc = MCMC(
sampler=NUTS(handl.condition(model, {"obs": rvs})),
num_warmup=1_000,
num_samples=1_000,
num_chains=4,
)
rng_key, rng_key_ = random.split(rng_key)
mcmc.run(rng_key_, n_obs=len(rvs))
mcmc.print_summary()
mcmc_samples = mcmc.get_samples()
# POSTERIOR PREDICTIVE
rng_key, rng_key_ = random.split(rng_key)
post_pred = Predictive(model, posterior_samples=mcmc_samples)(rng_key_, n_obs=1)
# PLOT GROUND TRUTH, OBSERVATIONS, PRIOR- AND POSTERIOR PREDICTIVES
fig, ax = plt.subplots()
ax.plot(x, y, label="ground truth pdf");
ax.hist(rvs, density=True, bins=80, histtype="step", label="observations");
ax.hist(prior_obs, density=True, bins=60, histtype="step", label="prior predictive");
ax.hist(post_pred["obs"].reshape(-1), density=True, bins=60, histtype="step", label="posterior predictive");
ax.legend();