MCMC for mixture of Gaussians

Misc.
1

Hi there! I’m new to pyro and I’m trying out a toy example of Dirichlet Process Mixture Model, implemented with truncation. I chose the prior for each component to have its own mean and covariance parameter, which are independently drawn. My model is like this:

T = 10
def mix_weights(beta):
    beta1m_cumprod = (1 - beta).cumprod(-1)
    return F.pad(beta, (0, 1), value=1) * F.pad(beta1m_cumprod, (1, 0), value=1)

def model(data):
    alpha = pyro.param("alpha", torch.tensor([1.0]))
    with pyro.plate("sticks", T-1):
        beta = pyro.sample("beta", Beta(1, alpha))
    with pyro.plate("component", T):
        mu = pyro.sample("mu", MultivariateNormal(torch.zeros(d), 5 * torch.eye(d)))
        cov = pyro.sample("cov", Wishart(df=d, covariance_matrix=torch.eye(d)))
    with pyro.plate("data", N):
        z = pyro.sample("z", Categorical(mix_weights(beta)))
        pyro.sample("obs", MultivariateNormal(mu[z], precision_matrix=cov[z]), obs=data)

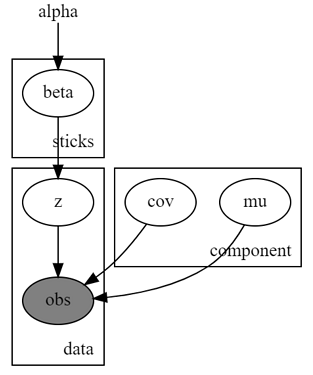
The graphical model may be more intuitive:

image
image478×571 9.91 KB

After this model construction, I tried to use MCMC sampling for posterior inference, with the following code:

nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_samples=500, warmup_steps=100)
mcmc.run(data)
posterior_samples = mcmc.get_samples()

However, this raises an error, which I thought should be related to the Wishart components in my model.

NotImplementedError: Cannot transform _PositiveDefinite constraints

How can I avoid this error? Should I change the prior, or use other methods like Cholesky decomposition to ensure the constraints implicitly?

Thanks for any advice!

2

We don’t have a bijective transform for PositiveDefinite constraint. It’s better to set a prior to the cholesky, like LKJCholesky prior. You can see an example here.

3

Oh I see, thanks! I didn’t even realize the problems with Wishart distribution until this time. I’ll go and learn about the LKJ distribution. Thanks!!

4

May I ask one more thing about prior on covariance and LKJ distribution? In my understanding, I should use LKJ cholesky to generate correlation matrix, and times another tensor to get a covariance matrix. My question is: How can this be effectively nested? For example, I need a prior on covariance matrix, and I hope this prior to be a mixture distribution (like this: Hierarchical Learning of Dimensional Biases in Human Categorization). In this case, I will need a Wishart sample to serve as scale matrix parameter in another Inverse-Wishart distribution. LKJ distribution simply defines a distribution (uniform) on correlation matrix. How can I use a hierarchical prior effectively?

Also, about the understanding of LKJ distribution, I’ve also read another short paper (https://arxiv.org/pdf/1809.04746.pdf), showing that LKJ distribution is equivalent to restricted Wishart distribution. Can I understand it as: the LKJ (times a scaling factor) is theoratically equivalent or similar (but numerically superior) to sampling from a Wishart distribution?