Hello,
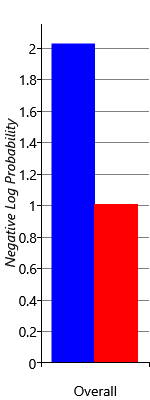
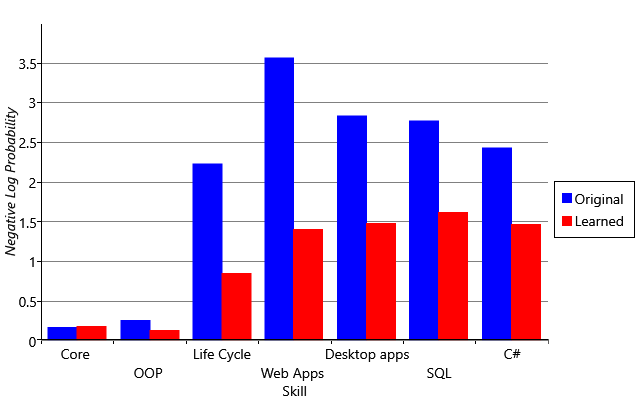
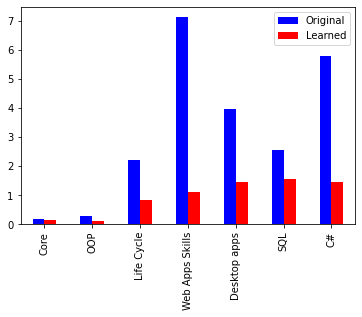
I am trying to reproduce Figure 2.29 from MBML chapter 2 showing the comparison of the log probabilities between two models and the log probabilities for each latent variable of interest.
What’s the best way to get the log probabilities from my model to make both panels shown in Figure 2.29?
I have seen other ways to get the log probability from this post, but I am seeing some errors.
-
potential_energyin MCMC.get_extra_fields results in anAttributeError: 'HMCGibbsState' object has no attribute 'potential_energy' -
log_densitySeems to work, but it only gives the total log probability, was expecting adictfrom each site within the trace -
log_densityseems to work formodel_00but not mymodel_02not sure why? Results in aValueError: Incompatible shapes for broadcasting: ((4000, 22), (1, 48))
The code can be found in this notebook, but I will post both models below and the function call from 3, showing the error.
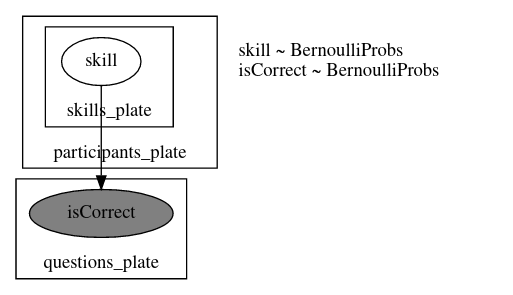
model_00
def model_00(
graded_responses, skills_needed: List[List[int]], prob_mistake=0.1, prob_guess=0.2
):
n_questions, n_participants = graded_responses.shape
n_skills = max(map(max, skills_needed)) + 1
participants_plate = numpyro.plate("participants_plate", n_participants)
with participants_plate:
skills = []
for s in range(n_skills):
skills.append(numpyro.sample("skill_{}".format(s), dist.Bernoulli(0.5)))
for q in range(n_questions):
has_skills = reduce(operator.mul, [skills[i] for i in skills_needed[q]])
prob_correct = has_skills * (1 - prob_mistake) + (1 - has_skills) * prob_guess
isCorrect = numpyro.sample(
"isCorrect_{}".format(q),
dist.Bernoulli(prob_correct).to_event(1),
obs=graded_responses[q],
)
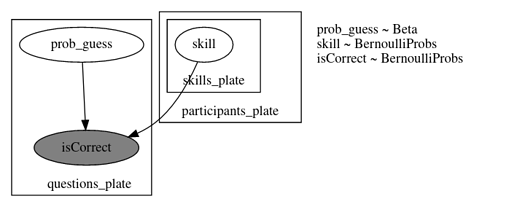
model_02 Incompatible shapes for broadcasting
def model_02(
graded_responses, skills_needed: List[List[int]], prob_mistake=0.1,
):
n_questions, n_participants = graded_responses.shape
n_skills = max(map(max, skills_needed)) + 1
with numpyro.plate("questions_plate", n_questions):
prob_guess = numpyro.sample("prob_guess", dist.Beta(2.5, 7.5))
participants_plate = numpyro.plate("participants_plate", n_participants)
with participants_plate:
skills = []
for s in range(n_skills):
skills.append(numpyro.sample("skill_{}".format(s), dist.Bernoulli(0.5)))
for q in range(n_questions):
has_skills = reduce(operator.mul, [skills[i] for i in skills_needed[q]])
prob_correct = has_skills * (1 - prob_mistake) + (1 - has_skills) * prob_guess[q]
isCorrect = numpyro.sample(
"isCorrect_{}".format(q),
dist.Bernoulli(prob_correct).to_event(1),
obs=graded_responses[q],
)
nuts_kernel = NUTS(model_02)
kernel = DiscreteHMCGibbs(nuts_kernel, modified=True)
mcmc_02 = MCMC(kernel, num_warmup=200, num_samples=1000, num_chains=4)
mcmc_02.run(rng_key, jnp.array(responses), skills_needed)
mcmc_02.print_summary()
log_density_model_02 = log_density(model_02, (jnp.array(responses), skills_needed), dict(prob_mistake=0.1), mcmc_02.get_samples())
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-16-ea553e8b7401> in <module>
----> 1 log_density_model_02 = log_density(model_02, (jnp.array(responses), skills_needed), dict(prob_mistake=0.1), mcmc_02.get_samples())
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/numpyro/infer/util.py in log_density(model, model_args, model_kwargs, params)
51 """
52 model = substitute(model, data=params)
---> 53 model_trace = trace(model).get_trace(*model_args, **model_kwargs)
54 log_joint = jnp.zeros(())
55 for site in model_trace.values():
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/numpyro/handlers.py in get_trace(self, *args, **kwargs)
163 :return: `OrderedDict` containing the execution trace.
164 """
--> 165 self(*args, **kwargs)
166 return self.trace
167
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/numpyro/primitives.py in __call__(self, *args, **kwargs)
85 return self
86 with self:
---> 87 return self.fn(*args, **kwargs)
88
89
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/numpyro/primitives.py in __call__(self, *args, **kwargs)
85 return self
86 with self:
---> 87 return self.fn(*args, **kwargs)
88
89
<ipython-input-12-472123f85406> in model_02(graded_responses, skills_needed, prob_mistake)
17 for q in range(n_questions):
18 has_skills = reduce(operator.mul, [skills[i] for i in skills_needed[q]])
---> 19 prob_correct = has_skills * (1 - prob_mistake) + (1 - has_skills) * prob_guess[q]
20 isCorrect = numpyro.sample(
21 "isCorrect_{}".format(q),
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in deferring_binary_op(self, other)
5867 if not isinstance(other, _scalar_types + _arraylike_types + (core.Tracer,)):
5868 return NotImplemented
-> 5869 return binary_op(self, other)
5870 return deferring_binary_op
5871
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in fn(x1, x2)
428 def _maybe_bool_binop(numpy_fn, lax_fn, bool_lax_fn, lax_doc=False):
429 def fn(x1, x2):
--> 430 x1, x2 = _promote_args(numpy_fn.__name__, x1, x2)
431 return lax_fn(x1, x2) if x1.dtype != bool_ else bool_lax_fn(x1, x2)
432 return _wraps(numpy_fn)(fn)
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in _promote_args(fun_name, *args)
324 _check_arraylike(fun_name, *args)
325 _check_no_float0s(fun_name, *args)
--> 326 return _promote_shapes(fun_name, *_promote_dtypes(*args))
327
328 def _promote_args_inexact(fun_name, *args):
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in _promote_shapes(fun_name, *args)
244 if config.jax_numpy_rank_promotion != "allow":
245 _rank_promotion_warning_or_error(fun_name, shapes)
--> 246 result_rank = len(lax.broadcast_shapes(*shapes))
247 return [broadcast_to(arg, (1,) * (result_rank - len(shp)) + shp)
248 for arg, shp in zip(args, shapes)]
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/util.py in wrapper(*args, **kwargs)
184 return f(*args, **kwargs)
185 else:
--> 186 return cached(config._trace_context(), *args, **kwargs)
187
188 wrapper.cache_clear = cached.cache_clear
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/util.py in cached(_, *args, **kwargs)
177 @functools.lru_cache(max_size)
178 def cached(_, *args, **kwargs):
--> 179 return f(*args, **kwargs)
180
181 @functools.wraps(f)
~/anaconda3/envs/numpyro_play/lib/python3.8/site-packages/jax/_src/lax/lax.py in broadcast_shapes(*shapes)
90 result_shape = _try_broadcast_shapes(shapes)
91 if result_shape is None:
---> 92 raise ValueError("Incompatible shapes for broadcasting: {}"
93 .format(tuple(map(tuple, shapes))))
94 return result_shape
ValueError: Incompatible shapes for broadcasting: ((4000, 22), (1, 48))