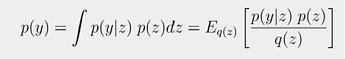Hello,
I need to compute the log posterior probability of latent variables in my model using a continuous SVI autoguide. The priors in my model are constrained to be positive, so the SVI autoguide distribution that I can get from guide.log_posterior will exist in an unconstrained space. I haven’t been able to accomplish this, but I know there are two ways to do this.
First, I can use the guide’s bijective transformation to transform the latent variables from the constrained space to the unconstrained space. From here, I can use guide.log_posterior to compute the log probability. Second, I can obtain the log probability corresponding to variables in the constrained space. I think this is done when computing the ELBO during an SVI fit.
Summary: How can I compute the log probability of latent variables using an SVI autoguide as my posterior distribution?
Hi @edwarddramirez, do you want to compute p(z) given that z is drawn from the guide q(z)? If so, the autoguide has a method sample_posterior to sample z. Then you can use log_density to compute p(z). Assuming you have a generative model p(z, y) = p(y|z)p(z) with y observed, you can use a block handler to ignore p(y|z) in log_density computation: something like block(model, hide=["y"]). I’m not sure how constrained space is related to your question. Could you clarify?
Hey @fehiepsi! I want to do something slightly different. I’ve made a bit more progress, but I haven’t finished. Let me describe my problem in more detail to clarify things.
Problem: I’m trying to implement Bayesian Model Averaging for different models fitting to the same data. This requires computing the log-evidence, p(y), for each model. I was planning on estimating it via the sample average:
Approach: I can compute the likelihood p(y|z) and the prior p(z) corresponding to a given sample z. I can’t compute q(z) because I don’t have the log-probability of the guide. However, I can compute the log-probability of the guide with respect to the unconstrained latent space, q(u). Therefore, my current strategy is to first draw the unconstrained latent samples u_samples using the distribution guide.get_posterior(params) and then convert to convert u → z with guide._unpack_and_constrain(u_samples, params) . This allows me to compute p(y|z), p(z), and q(u) corresponding to each sample u. The final step is to calculate q(z) ∝ q(u), requiring the log-jacobian-determinant of the map that takes u → z. This leads to the following questions.
Questions:
- Does this approach make sense to you?
- How can I calculate the required
log_abs_det_jacobian? I see that I can call this from a numpyro.distributions.transforms class. I’m just unsure if the transform (or its inverse) that I can get from guide.get_transform is the right one to use.
I think you can compute log density of the guide using log_density utility. Are you using sort of guide.base_dist to compute the log probability? If you, you are right that log-jacobian is needed.
I think I got log_density to work correctly. I had issues because I didn’t seed the guide before computing it. However, log_density computes the log probability corresponding to a single sample that is generated within the seed.
How can I use log_density to calculate the log probability corresponding to many drawn samples? I want to use the same samples to calculate log_density of the guide and the model.
You can checkout the lovely jax.vmap 
I tried it out. But I ran into some tracer leakage. For now, I’ll just jit the log_density and use a for loop. It might be fast enough for my purposes. Thanks for all the help! 
I assume you put the seed handler outside of vmap? The vmap body function should be closed, i.e. meaning that it does not depend on some global seed handler. You can do something like vmap(lambda key, sample: log_density(seed(guide, key), …))(keys, samples) where keys = random.split(random.PRNGKey(0), num_samples)
I didn’t put the seed handler outside the map 
. You are correct. Placing it outside fixes the issue and allows for much faster calculations!
Hey, I know this was a while ago but I’m trying to do something similar and for some reason can’t quite sort it out. Would you happen to be able to share the code snippet you got to work with vmap and log_density to evaluate the guide log density at samples? Much appreciated!
Hi Natalie. Try taking a look here. The link takes you to a notebook that I made for implementing Bayesian Model Averaging with NumPyro. What you are looking for is in the cells under the markdown cell labelled Compute the Evidence for Each Model.
If you want to run the code, consider following the instructions in the repo to install the required dependencies.
Hope it helps!
