Hello there,
I am working on a latent variable model with the following form:
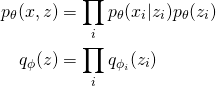
Here p is my model, with fixed global parameters theta, while q is my mean-field guide with local variational parameters phi_i.
To speed up learning, I want to perform subsampling on the indexes i, which is very close to stochastic variational inference as presented in http://www.jmlr.org/papers/volume14/hoffman13a/hoffman13a.pdf (except that for them theta is a random variable, corresponding to an additional global term in the guide).
My problem is that I don’t know how to tell Pyro the following: my goal is to learn the global parameter theta, and for this learning phase I don’t care about the local variational parameters phi_i. I only want to perform gradient ascent on theta, and compute a batch of phi_i in the background to get a (twice) noisy estimate of the gradient. Is this built in Pyro? Do I have to declare all of the phi_i as parameters nonetheless?
Thanks in advance
Giom
[EDIT] Could it have something to do with this issue: Params inside iarange · Issue #238 · pyro-ppl/pyro · GitHub ?
My problem is that I don’t know how to tell Pyro the following: my goal is to learn the global parameter theta , and for this learning phase I don’t care about the local variational parameters phi_i . I only want to perform gradient ascent on theta , and compute a batch of phi_i in the background to get a (twice) noisy estimate of the gradient.
can you explain what this means? i’m have a hard time parsing what you want (mathematically)
Thanks for your answer,
Basically, my question was about the behavior of local v. global variational parameters in Pyro.
For instance, in the incomplete code of SVI Part II: Conditional Independence, Subsampling, and Amortization — Pyro Tutorials 1.8.4 documentation, I was wondering what happens to the parameters used within a subsampled plate (the lambda_i) as opposed to the ones defined globally (for instance the mean of beta): I think it would help users if that part was more detailed in the doc.
After testing, it seems that only the lambda_i corresponding to subsample indices are updated at each SVI step, along with loc_beta: that is indeed logical and coherent with your source https://cims.nyu.edu/~rajeshr/papers/ranganath14-supp.pdf.
My question came from the fact that in several papers I found (including the one I cited above), SVI was presented as a generalization of coordinate ascent for mean field, in which case it alternates between:
-
Optimizing of a batch of local parameters to get
phi_batch^*
- Performing a gradient step on the global parameter based on
phi_batch^*, and then forgetting about the local ones we just computed.
But I guess the coordinate ascent is simply a different setting which doesn’t apply well to black-box ELBO.
yes, you basically answered your own question. we use the term ‘stochastic variational inference’ in a more general sense than it is sometimes used in the literature (stochastic either because of data subsampling or because of sampling latent variables or both). often in the literature ‘svi’ refers to the data subsampling case (all latent variables are integrated out in the mean field updates)