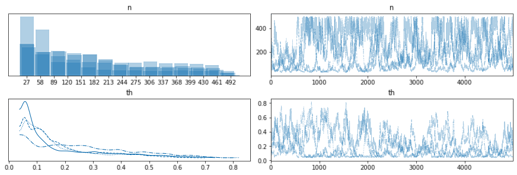
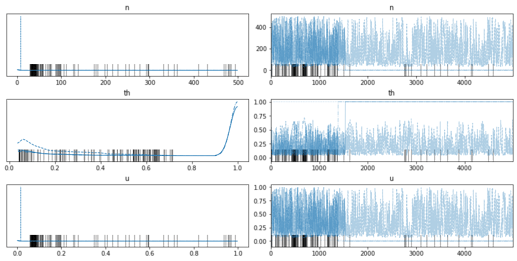
It seems numpyro can model latent integers using funsor, great. In this example I want to model 2 latent groups using Dirichlet and Categorical.
I am struggling with the ii variable, which needs to be length N=100. I tried various shape parameters but I failed.
I previously got this to work in pymc3 but am curious how to do it in numpyro.
# pip install funsor
import jax.numpy as np
import numpyro
import numpy.random as npr
import numpyro.distributions as dist
from jax import random, ops
from numpyro.infer import MCMC, NUTS
N = 100
x = npr.normal(size=N)
alpha = np.array([1., 1.]) # prior
group = npr.choice(2, size=N, p=[.7, .3]) # unequal groups
y = 10 + 4 * (group == 0) + x + npr.normal(size=N)
print(group)
print(y.mean())
def model(x=None, y=None, alpha=None):
a = numpyro.sample('a', dist.Normal([10, 0], 10))
b = numpyro.sample('b', dist.Normal(0, 1))
sigma = numpyro.sample('sigma', dist.Gamma(1, 1))
theta = numpyro.sample('theta', dist.Dirichlet(alpha))
# ii should be length N
ii = np.ones(N)
# ii = numpyro.sample('ii', dist.Categorical(theta))
for i in range(N):
ops.index_update(ii, i, numpyro.sample('ii' + str(i), dist.Categorical(theta)))
pred = numpyro.sample('pred', a[ii] + b * x, sigma, obs=y)
# print(dist.Dirichlet(np.repeat(2, 7)).sample(random.PRNGKey(1805), (10,)))
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_warmup=500, num_samples=1000, num_chains=1)
rng_key = random.PRNGKey(0)
mcmc.run(rng_key, x=x, y=y, alpha=alpha)
mcmc.print_summary()
posterior = mcmc.get_samples()
print(posterior)