Keep latent discrete parameters consistent

numpyro
1

I’m trying to learn how to infer discrete latent variables from observed continuous data properly in numpyro. The basic example I’m attempting to do is a distribution of heights where the sex of the observation is unknown and inferred.

Here is the code to generate the data.

import pandas as pd
import numpy as np
import jax.numpy as jnp
import numpyro
from numpyro.infer import MCMC, NUTS, HMC, MixedHMC
import numpyro.distributions as dist
from jax import ops, random, vmap
import arviz as az
import jax
import seaborn as sns

import os
os.environ['XLA_FLAGS'] = '--xla_force_host_platform_device_count=6'
numpyro.set_host_device_count(4)

N = 100
var_num = 2
with numpyro.handlers.seed(rng_seed=0):
    mixing_dist = dist.Categorical(probs=jnp.ones(var_num) / var_num)
    component_dist = dist.Normal(loc=jnp.array([5*12+10, 5*12+4]), scale=jnp.array([3, 2]))
    mixture = dist.MixtureSameFamily(mixing_dist, component_dist).expand([N])
    y = mixture.sample(jax.random.PRNGKey(42))

sns.histplot(y)

And here are two different models to estimate the model:

def model3(heights):
    num_classes = 2
    N = len(heights)
    with numpyro.plate('class', num_classes):
        mu = numpyro.sample(
            'mu',
            dist.Normal(0, 100).expand([num_classes])
        )
        sigma = numpyro.sample(
            'sigma', 
            dist.HalfNormal(10).expand([num_classes])
        )
    
    with numpyro.plate('items', N):
        pi = numpyro.sample("pi", dist.Beta(0.5, 0.5))
        c = numpyro.sample('mixing_dist', dist.Bernoulli(probs=pi))

        numpyro.sample(
            'component_dist',
            dist.Normal(loc=mu[c], scale=sigma[c]),
            obs=heights
        )

kernel = MixedHMC(HMC(model3))
m = MCMC(kernel, num_warmup=8000, num_samples=2000, num_chains=4, progress_bar=True)

m.run(random.PRNGKey(2), y)

samples = m.get_samples()
data = az.from_numpyro(m)

az.plot_trace(data, var_names=['mu', 'sigma'])
az.summary(data, var_names=['mu', 'sigma'])

And also this (which is more easily extended past the 2 class case):

def model4(heights):
    num_classes = 2
    N = len(heights)
    with numpyro.plate('class', num_classes):
        mu = numpyro.sample(
            'mu',
            dist.Normal(0, 100).expand([num_classes])
        )
        sigma = numpyro.sample(
            'sigma', 
            dist.HalfNormal(10).expand([num_classes])
        )
    
    with numpyro.plate('items', N):
        pi = numpyro.sample("pi", dist.Dirichlet(jnp.ones(num_classes)))
        c = numpyro.sample('mixing_dist', dist.Categorical(probs=pi))

        numpyro.sample(
            'component_dist',
            dist.Normal(loc=mu[c], scale=sigma[c]),
            obs=heights
        )

kernel = MixedHMC(HMC(model4))
m = MCMC(kernel, num_warmup=8000, num_samples=2000, num_chains=4, progress_bar=True)

m.run(random.PRNGKey(2), y)

samples = m.get_samples()
data = az.from_numpyro(m)

az.plot_trace(data, var_names=['mu', 'sigma'])
az.summary(data, var_names=['mu', 'sigma'])

Both of those seem to work (although the second one gives some warnings). However the r_hats are not good, because which category represents male and female can switch places within different chains.

	        mean	sd	    hdi_3%	hdi_97%	mcse_m mcse_sd	blk	tail	r_hat
mu[0]	    67.703	3.281	63.955	71.907	1.618	1.237	6.0	149.0	1.74
mu[1]	    67.666	3.205	63.991	71.771	1.579	1.207	6.0	129.0	1.74
sigma[0]	2.315	0.546	1.532	3.388	0.186	0.136	9.0	200.0	1.37
sigma[1]	2.358	0.562	1.554	3.423	0.197	0.144	8.0	126.0	1.41

mcmc

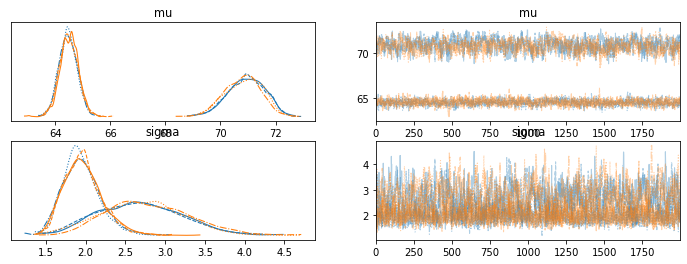
Is there a better way to handle this to get consistent labeling of the discrete variables so the r_hats aren’t thrown off by different index assignments to the latent variables? Would it be better to frame the second mu as being the first mu plus some positive only parameter? And how to move to 3+ classes and retain consistency?

Also, is there a way to do inference with MixtureSameFamily? I couldn’t get that to work. I would get an error message:
ValueError: The mixing distribution need to be a numpyro.distributions.Categorical. However, it is of type <class 'jax.interpreters.partial_eval.DynamicJaxprTracer'>

2

I don’t know how to deal with label switching issues. Probably you want to specify priors in some ways or do postprocessing your chains. Maybe using some ordered prior on mu? (e.g. dist.TransformedDistribution(dist.Normal(0, 100).expand(...), dist.transforms.OrderedTransform())).

For your model, I would prefer using enumeration with infer_discrete as in the annotation example.

do inference with MixtureSameFamily ?

Could you provide some reproducible code?

3

When I change the model to:

def model6(heights):
    num_classes = 2
    N = len(heights)
    with numpyro.plate('class', num_classes):
        mu = numpyro.sample(
            'mu',
            dist.TransformedDistribution(
                dist.Normal(0, 100).expand([num_classes]), 
                dist.transforms.OrderedTransform()
            )
        )
        sigma = numpyro.sample(
            'sigma', 
            dist.HalfNormal(10).expand([num_classes])
        )
    
    with numpyro.plate('items', N):
        pi = numpyro.sample("pi", dist.Beta(0.5, 0.5))
        c = numpyro.sample('mixing_dist', dist.Bernoulli(probs=pi))
        numpyro.sample(
            'component_dist',
            dist.Normal(loc=mu[c], scale=sigma[c]),
            obs=heights
        )

I get this error:

ValueError: Incompatible shapes for broadcasting: ((1, 1), (100, 2), (1, 100))

If I use an ellipsis, it complains that is not iterable.

The infer_discrete example seems to use it within the Predictive class after sampling with NUTS. Should I just be using NUTS instead of MixedHMC for a problem like this?

4

Maybe you need Vindex as in annotation example? Something like

loc=Vindex(mu)[..., c], scale=Vindex(sigma)[..., c]

It seems to me that your mu has shape (num_classes, num_classes) while your sigma has shape (num_classes). Is it intended?