Issue with optimizing HMM with Gaussian Emissions

1

I’m using an HMM to perform gesture recognition trained on several keypoints of the body. The model is something like

mu_i ~ N(0, 3)
sig_i ~ LogNormal(-3, 1)
transition_i ~ Dirichlet(15)

x_0 = 0
x_i ~ Cat(transition_{i-1})
y_i ~ N(mu_{x_i}, sig_{x_i})

However, when I train the HMM, the HMM ends throwing out all but one state. I’ve managed to repro the issue training just the emission center with a model as follows:

    @config_enumerate
    def model(data):
        data = data.float()
        num_cls = data.shape[0]
        num_copies = data.shape[1]
        num_dimensions = data.shape[3]
        num_time = data.shape[2]
        num_states = transition_matrix.shape[0]

        with pyro.plate("num_cls", num_cls) as cls_idx:
            with pyro.plate("hmm_gen", num_states - 1):
                with pyro.plate("hmm_dim", num_dimensions):
                    emission_mus = pyro.sample('emission_mus',
                                                           distributions.Uniform(torch.tensor(-3.0), torch.tensor(3.0)))

            with pyro.plate("copies", num_copies) as copies:
                state = torch.zeros(num_copies, num_cls).long()
                dimension_plate = pyro.plate("hmm_dim_gen", num_dimensions, dim=-3)
                for t in pyro.markov(range(num_time)):
                    with dimension_plate as d:
                        emission_mu = Vindex(emission_mus)[d.unsqueeze(-1).unsqueeze(-1), state, cls_idx]
                        emission_sigma = Vindex(emission_sigmas)[d.unsqueeze(-1).unsqueeze(-1), state, cls_idx]
                        emission = pyro.sample("y_{}".format(t), distributions.Normal(emission_mu, emission_sigma),
                                               obs=data[:, :, t].T)
                    state = pyro.sample("x_{}".format(t + 1),
                                        distributions.Categorical(Vindex(transition_matrix)[state, cls_idx]))

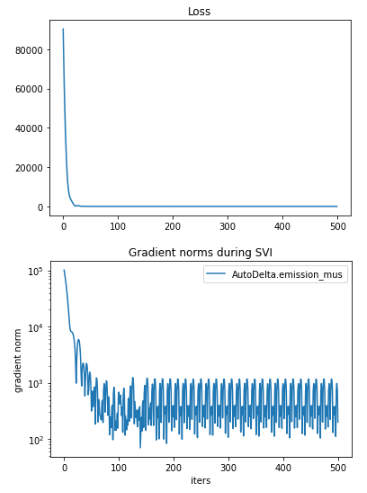
The full repro code can be seen at Full Code For Issue - Pastebin.com which also includes some sample data and the full training code. Anyway, when trained with this, it appears to train fine:
losses

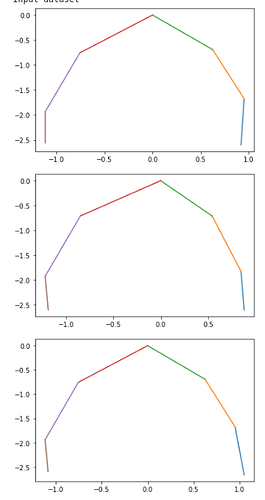
but, when the input dataset is visualized

input_dataset
input_dataset366×688 28.4 KB

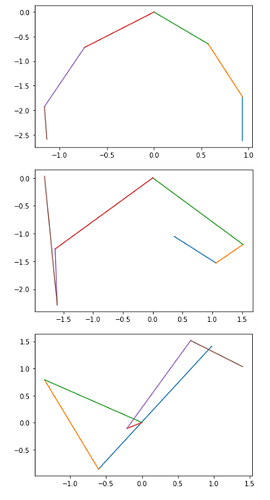
vs the learned center of the state emissions

learned_clusters
learned_clusters374×691 32.9 KB

You can observe that only the first state is used. This causes issues when using the model generatively as the transition matrix still transitions to the clusters which are not learned. I’m curious if this is the expected behavior of the SVI under the EnumElbo loss, and if so, if there’s any workaround to get all states to properly train? Thanks!

2

Hi @npw,
my guess is that clusters are being poorly initialized by the default strategy init_loc_fn=init_to_median, and then all but one cluster get nearly zero weight. You might try to initialize cluster means to randomly chosen data points, something like

def init_loc_fn(site):
    if site["name"] == "emission_mus":
        num_cls = site["fn"].shape()[-1]
        # I don't know the train_ds_tensor dimension meanings, so I'm
        # arbitrarily indexing on the first dim; you'll need to fix this.
        random_ids = torch.multinomial(
            torch.ones(len(train_ds_tensor)), num_cls replacement=False
        )
        return train_ds_tensor.index_select(0, random_ids)
    # fall back to default strategy
    return init_to_median(site)

guide = AutoDelta(model, init_loc_fn=init_loc_fn)

You might also try first training while constraining cluster weights to be uniformly 1 / num_clusters, then warm-starting with that but allowing cluster weights to be learned.

3

Hi @fritzo,
thanks so much for your response!

Because the transition matrix is hardcoded to

transition_matrix = torch.tensor([[[0.3375, 0.3312, 0.3312]],
    [[0.3333, 0.3333, 0.3333]],
    [[0.3333, 0.3333, 0.3333]]])

in the full code example (https://pastebin.com/HRi45Q3t ), and is not learned, shouldn’t all states/clusters be used (and therefore, all cluster centers should be semi-reasonable)?

4

Oh, yes all the clusters should be used if you hard-code the state transition matrix.

BTW I notice that your state transition matrix is nearly memoryless: each state has nearly uniform probability of transitioning to each other. I’m unsure whether an HMM will be useful in a model where there is nearly zero memory. Is that transition matrix indeed your intent?

5

Yup! So I’m just using this transition matrix as a stand-in dummy until I figure out the issue, I’ll then actually have it learn a useful matrix. Does anything else about the code seem off, or should I file an issue if this appears to be unexpected behavior. Thanks!

6

friendly bump @fritzo (on if I should file an issue)

7

Hi @npw, have you tried better initialization of emission distributions, e.g. initialization from randomly chosen data points or initialization from k-means?