Hi all,
I have been working with some model which I have been able to simplify for demonstration purposes. This is optimising a single parameter now.
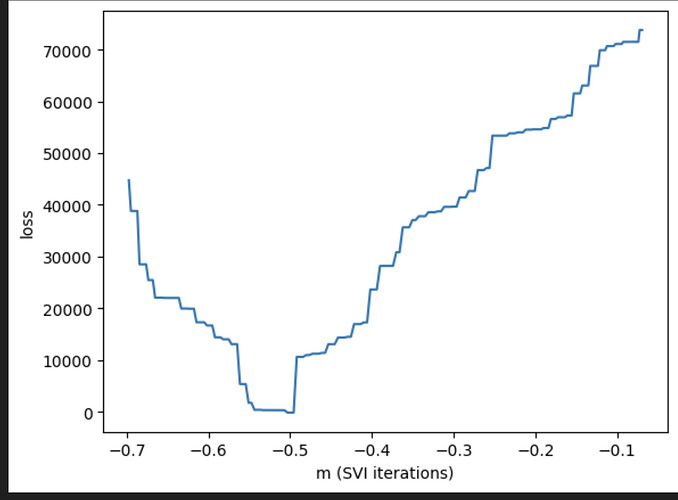
The point is that, as the SVI optimisation goes on, the loss decreases as it should, reaches a minimum at the ground truth parameter value, BUT then keeps going, making it worse and worse. Sorry if this is a silly question, but, shouldn’t it just stay low and converge?
In a bit more detail, this is a regression model where data points are given in sequence, and at some point of the sequence, the regression coefficients change. Assuming we know the before- and after-change values of the regression coefficient, the goal is to find when it changes. This is the loss curve, and the right value is -0.5, where it rightfully reaches a minimum. Why doesn’t it stop?
The code I’m using to recreate this is:
N,p = 200,6 # time points and features
mtrue = -0.5 # this is the thing we want to infer, which range is [-1.0,1.0],
# where -1.0 represents the first time point, and +1.0 the last one.beta1 = torch.normal(torch.zeros(p),torch.ones(p)) # we’ll assume we know beta1 and beta2
beta2 = torch.normal(torch.zeros(p),torch.ones(p))
betatrue = torch.zeros((N,p))
r = torch.linspace(-1.0,1.0,N)
for j in range(N):
if r[j] <= mtrue: betatrue[j,:] = beta1
else: betatrue[j,:] = beta2X = torch.normal(torch.zeros((N,p)),torch.ones((N,p)))
y = torch.sum(X * betatrue,1) + 0.1 * torch.normal(torch.zeros(N),torch.ones(N))def model(X,y):
m = pyro.sample("m",dist.Normal(0,10)) beta = torch.zeros((N,p)) for j in range(N): if r[j] <= m: beta[j,:] = beta1 else: beta[j,:] = beta2 mean_obs = torch.sum(X * beta,1) sigma_obs = 0.1 * torch.ones(1) with pyro.plate("plate_data", N): obs = pyro.sample("obs",dist.Normal(mean_obs, sigma_obs), obs=y)def guide(X,y):
mean_m_hat = pyro.param("mean_m_hat", -0.7 * torch.ones(1), constraint=constraints.interval(-1.0, +1.0)) q_m = pyro.sample("m",dist.Delta(mean_m_hat))def train():
pyro.clear_param_store() adam = pyro.optim.Adam({"lr": 0.01}) svi = SVI(model, guide, adam, loss=Trace_ELBO()) loss_list = [] m_list = [] for step in range(200): loss = svi.step(X,y) loss_list.append(loss) print('[iter {}] loss: {:.4f}'.format(step, loss)) m_list.append(pyro.param("mean_m_hat").detach().numpy()[0]) return loss_list,m_list
Many thanks. Pyro is fun