Hi, I am currently implementing a version of the ORDScale Model described in this paper. The corresponding graph is:
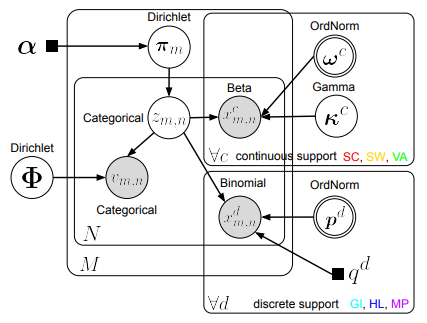
Disregard the discrete support plate in the bottom-right, it is not relevant to my use case.
The goal of the model is to infer latent classes z_m of documents m given the words v and the sentiment values x.
class OrdScale(nn.Module):
def __init__(self, n_c=5, vocab_size=corpus["vocab_size"], device=device, verbose=False):
super().__init__()
self.n_c = n_c # number of classes
self.vocab_size = vocab_size
self.device = device
self.verbose = verbose
def model(self, X, V, pi_Z):
n_stories, n_words = X.shape
base_X_c = dist.Normal(torch.zeros(self.n_c, device=self.device), torch.ones(self.n_c, device=self.device)/n_stories)
mode_X_c = pyro.sample(
"mode_X_c",
dist.TransformedDistribution(base_X_c, [transforms.OrderedTransform(), transforms.SigmoidTransform()])
)
conc_X_c = pyro.sample("conc_X_c", dist.Gamma(torch.ones(self.n_c, device=self.device), torch.ones(self.n_c, device=self.device)).to_event(1))
Phi = pyro.sample("Phi", dist.Dirichlet(torch.ones(self.n_c, self.vocab_size, device=self.device)/self.vocab_size).to_event(1))
with pyro.plate('document_plate', n_stories, dim=-2):
pi_Z = pyro.sample("pi_Z", dist.Dirichlet(torch.ones(self.n_c, device=self.device)/self.n_c), obs=pi_Z)
with pyro.plate('word_plate', n_words, dim=-1):
Z = pyro.sample('Z', dist.Categorical(pi_Z))
mode_X_c_n = Vindex(mode_X_c)[..., Z.long()]
conc_X_c_n = Vindex(conc_X_c)[..., Z.long()]
X = pyro.sample('X', dist.Beta(
(mode_X_c_n * conc_X_c_n) + 1 , ((1 - mode_X_c_n) * conc_X_c_n) + 1 ), obs=X
)
Phi_n = Vindex(Phi)[..., Z.long(), :]
V = pyro.sample('V', dist.Categorical(Phi_n), obs=V)
return pi_Z, Z
def guide(self, X, V, pi_Z):
n_stories, n_words = X.shape
alpha = pyro.param('alpha', lambda: torch.ones(self.n_c, device=self.device)/self.n_c, constraint=constraints.positive)
base_X_c = dist.Normal(torch.zeros(self.n_c, device=self.device), torch.ones(self.n_c, device=self.device)/n_stories)
mode_X_c = pyro.sample(
"mode_X_c",
dist.TransformedDistribution(base_X_c, [transforms.OrderedTransform(), transforms.SigmoidTransform()])
)
conc_X_c = pyro.sample("conc_X_c", dist.Gamma(torch.ones(self.n_c, device=self.device), torch.ones(self.n_c, device=self.device)).to_event(1))
Phi = pyro.sample("Phi", dist.Dirichlet(torch.ones(self.n_c, self.vocab_size, device=self.device)/self.vocab_size).to_event(1))
with pyro.plate('document_plate', n_stories, dim=-2):
# pi_Z = pyro.sample("pi_Z", dist.Dirichlet(torch.ones(self.n_c, device=self.device)/self.n_c), obs=pi_Z)
pi_Z = pyro.sample("pi_Z", dist.Dirichlet(alpha))
with pyro.plate('word_plate', n_words, dim=-1):
Z = pyro.sample('Z', dist.Categorical(pi_Z))
However, after a few steps of SVI, the loss becomes infinite. I tried using dtype float64 and reducing batch size from 64 to 4 but it did not solve the problem (although reducing batch size seems to mostly postpone the infinite loss by a few batches).
While tinkering I sometimes had an error telling me that the log_prob_sum of pi_Z was infinite so the issue might be related to pi_Z. EDIT: actually, probably not, that was due to me feeding a tensor that contained the value 1. Changing it removed the warning.
Do you have an idea what causes it?
Also, if you spot errors in the implementation of my model and/or guide, please tell me.
Thank you for your attention.