Inference with discrete latent variables (Sequential SS-VAE)

[ffp]

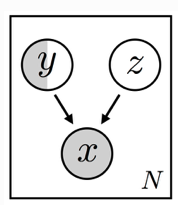
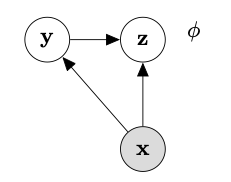
Hi everyone!

I’m new to both probabilistic programming and probabilistic machine learning in case you are wondering why I make stupid questions on this forum from time to time

I’m trying to implement a semi-supervised seq2seq VAE for sequential data by taking inspiration by both your semi-supervised VAE (SS-VAE) and DMM tutorials.

Unfortunately, now I’m stuck in one point of my code and I need, if possible, your help/educated advice.

Let me suppose that (part of ) the decoder is a RNN —actually are RNNs also the encoder_z and the encoder_y. The label y is a discrete variable, while z is a continuous one (i.e., a multivariate Gaussian). To avoid any issue due to the high variance of a Monte Carlo estimator for the discrete variable, I decided to use the same solution as in the SS-VAE tutorial, that is that of enumerating y.

A typical approach adopted in seq2seq models relies in concatenating z coming from the encoder_z and y coming from the encoder_y, mapping them into the RNN’s hidden size (e.g., through a MLP) and using it as initial hidden state for the RNN in the decoder, by letting this latter also receive the input x (i.e., some sequence of symbols) during the training.

However, as a consequence of the config_enum setting for the guide (used in conjunction with TraceEnum_ELBO), both y and z (sampled from their respective priors in the model part) have the following shape: y.shape = (num_classes, batch_size, num_classes), and z.shape = (num_classes, batch_size, latent_size). I concatenated z and y, passed the result to an MLP that returned the hidden_state of shape (num_classes, batch_size, hidden_size). At this point I have the doubt on how to proceed. Indeed, the RNN requires that the hidden_state has the shape (1, batch_size, hidden_size) —let me suppose, for the sake of simplicity, that the RNN is not bidirectional and the number of layers is equal to 1.

Thus, which is the more correct way to transform/reshape the hidden_state of shape (num_classes, batch_size, hidden_size) into the correct shape (1, batch_size, hidden_size) required to be fed into the RNN inside the decoder?

I hope that I was able to describe my doubt, even without using code snippets.

Thank you in advance for your help!

[martinjankowiak]

hello ffp, i’m afraid that “semi-supervised seq2seq VAE for sequential data” is too imprecise a description for me to follow. can you provide more details? what latent variables are in the model? what plates? how is the guide structured? etc.

[ffp]

Dear Martin,
thank you for your reply.

I was almost sure that the description was too much vague, but being more precise implies putting here a lot of code and it seemed to me unpractical.

I hoped that the reference to your SS-VAE tutorial could help me avoiding this. Is there any alternative solution to that of reporting here hundreds of code lines? What about, e.g., providing you with a link to an external repo?

[martinjankowiak]

hello,

i didn’t say anything about code: words suffice. realistically no one wants to look at hundreds of lines of someone else’s code. simply describe the graphical structure of your model and guide.

[ffp]

Ok. I will try to express my problem by words, but it is not easy at all.

The graphical structure of the model is the following:

The latent y is discrete and represents the labels (modeled with a OneHotCategorical distribution); the latent z is a continuous variable instead (modeled with a multivariate Gaussian). The only particularity is that x is a discrete sequence of symbols, and its generation is through a Categorical distribution with a number of classes equal to the number of symbols into the vocabulary. Specifically, at each time step of the sequence x, I generate a symbol by means of a Categorical distribution.

As far as it pertains the guide, the inference model is:

As in the SS-VAE tutorial, the approximate posterior q(z, y| x) is factorized into q(z |y, x) and q(y | x) .
A sort of meta-code for the guide I defined is reported below:

def guide(self, xs, ys=None, annealing_factor):
    
	length = ...
	
	pyro.module("ss_vae", self)
    with pyro.plate("data", xs.size(0)):
        if ys is None:
        	#q(ys |xs_{1:T})
            cat_params = self.encoder_y(xs, length)
            ys = pyro.sample("y", dist.OneHotCategorical(cat_params))

        # q(z | ys, xs_{1:T})
        z_loc, z_scale = self.encoder_z(xs, ys, length)
        z_dist = dist.Normal(z_loc, z_scale)
        with pyro.poutine.scale(scale=annealing_factor):
                pyro.sample("z", z_dist.to_event(1)) 

The main loss (let me suppose that I’m not using the auxiliary one at this moment) is defined as in the following:

guide = config_enumerate(ss_vae.guide, "parallel", expand=True)
elbo = TraceEnum_ELBO(max_plate_nesting=1, strict_enumeration_warning=False)
svi_main = SVI(ss_vae.model, guide, optimizer, loss=elbo)

My doubt is what to do in the decoder that generates the probabilities for the categorical likelihood p(x_{1:T} | y, z). The decoder is basically a RNN and I need to provide it with an initial hidden state and an input. As said before, a typical approach in seq2seq models consists in concatenating y and z, passing this concatenation to an MLP to have the same hidden size specified for the RNN and using it as initial hidden state.

However, y and z because of the enumeration in the guide, have the following shape: y.shape =(num_labels, batch_size, num_labels) and z.shape = (num_labels, batch_size, latent_size) --the first dimension is the dimension allocated to use the enumeration. If I concatenate them I will have a tensor of shape (num_labels, batch_size, latent_size + num_labels). After passing it through an MLP, I have a tensor of shape (num_labels, batch_size, hidden_size). This latter tensor should be provided to the RNN as initial hidden state, but the hidden state must have a shape (if the the RNN is not bidirectional and the number of layers is 1) with a form (1, batch_size, hidden_size) instead.

Since the enumeration is managed directly by Pyro, I’m wondering how I can safely transform the tensor of shape (num_labels, batch_size, hidden_size) into one with shape (1, batch_size, hidden_size) to be fed into the decoder without hindering the correct computation of the loss.

Actually, in your tutorial on SS-VAE there is no problem like this since the concatenation of y and z is passed trough a MLP that “preserves” the shape, unless of the last dimension that is mapped into the input size (784 since are MNIST images 28x28).

[martinjankowiak]

if i understand your setup correctly you need to reshape the output of your MLP to have shape (num_labels x batch_size, hidden_size). then you can pass it through the RNN. then you can reshape the output so that the two leading dimensions are (num_labels, batch_size). in other words i don’t believe you need to do anything special on the pyro side. you just need to reshape things consistently on the torch side and work around the torch API.

[ffp]

Thank you for your reply.

However, sorry, I didn’t fully understand your suggestion. As a matter of fact a tensor of shape
(num_labels x batch_size, hidden_size) cannot be used as hidden state for a RNN since this requires a shape of of (1, batch_size, hidden_size) —batch_size must be coherent (and then cannot be changed, I guess) with that of the input to the RNN that must have a shape (batch_size, sequence_length, input_size) when the option of the RNN batch_first is set to True.

Thus, does make sense to have a tensor with shape (1, batch_size, num_labels x hidden_size) and provide it to the RNN as hidden state instead ?

Or, as an alternative way that does not alter the hidden size of the RNN, could be the following a possible solution?

• reshape the original z from this shape (num_labels, batch_size, latent_size) to the new shape (1, batch_size, num_labels x latent_size) and y from the shape (num_labels, batch_size, num_labels) to the new shape (1, batch_size, num_labels x num_labels);

• concatenate them to form a tensor of shape (1, batch_size, num_labels x latent_size + num_labels x num_labels) and pass it through a MLP that returns a tensor of shape (1, batch_size, hidden_size) that I can actually use as hidden state for the RNN;

• reshape z and y to their original shapes with (num_labels, batch_size) as leading dimensions.

What do you think about it? Is this envisaged solution totally wrong?

[ffp]

Unfortunately, the same solution I envisaged above does not work when y is observed (is not latent). As a matter of fact, in this case the shapes of z and y are (batch_size, hidden_size) and (batch_size, num_classes) , respectively. No problem in this case with the shapes and to provide the RNN with a hidden state having the right dimension.

I don’t know how to proceed.

What about using a sequential enumeration instead of the parallel one? Does this could avoid me to mess with the shapes?

Is there some alternative to the enumeration in Pyro to effectively deal with discrete latent variables?

[martinjankowiak]

the torch api should allow you to do what you need. conceptually each of the enumerated dimensions expands the batch dimensions: batch_size x num_classes. you just need to make sure that that there isn’t unwanted cross-talk: output[batch_i] of a MLP/RNN should only depend on input[batch_i]; and similarly for the enumerated dimension.

why can’t you shape the output of your MLP to have shape (1, num_labels x batch_size, hidden_size)?

it’s probably easiest to consider the case of observed and unobserved class label separately. i.e. alternate mini-batches with full observed or fully unobserved class labels

[ffp]

Thank you again for your reply.

What I don’t understand in your solution is that the RNN must receive a hidden state and an input. Let me suppose that the input comes from a DataLoader that provides me with batches of a fixed batch_size (e.g., 32). Thus, how can I pass to the RNN an hidden state and an input having shapes that differ for the batch_size?

To be concrete, let me use the following example:

#batch_size = 32 and hidden_size = 100, num_labels=2, h_in=50, seq_len = 40

rnn = nn.RNN(50, 100, batch_first=True)

#reshaped hidden state (1, num_classes x batch_size, hidden_size)
hidden = torch.randn(1, 2*32, 100)

#input shape = (batch_size, seq_len, h_in)
input = torch.randn(32, 40, 50)

output, hidden = rnn(input, hidden)

Of course this returns me with an error:

RuntimeError: Expected hidden size (1, 32, 100), got [1, 64, 100]

Did you mean this? Otherwise, in more simple words (and, if possible, through an example), can you explain me again your idea?

Sorry for bothering you…

[martinjankowiak]

i believe you need to expand your input by a factor of num_classes. basically you need to explicitly reshape/expand things along the way because torch can’t automatically figure out what your intentions are.

[ffp]

Thank you.

Then, do you suggest to allow the DataLoader to provide input with a shape (batch_size x num_classes, seq_len, h_in)?

Or do you suggest to change the input tensor (batch_size, seq_len, h_in) originally coming from the DataLoader instead?

In particular, I found a function in Pytorch (sorry, but I’m quite new also to Pytorch, since I was accustomed to Keras up to now) called torch.repeat. Is, in your educated opinion, correct to use it to expand the batch_size dimension of input of a factor num_classes? Specifically, by reusing the code in the example above this could amount to do as in the following:

input = torch.randn(32, 40, 50)
input = input.repeat(2,1,1)
input. shape = torch.Size([64, 40, 50])

In your opinion, is “semantically” correct to repeat the content to expand the batch_dimension by a factor num_classes?

As an equivalent way to proceed, what about the following one where I first expand the input tensor by a factor equal to num_classes in the leftmost dimension and then I reshape to put it in the desired shape (64, 40, 50)?

input = torch.randn(32, 40, 50)
input = input.expand(2,-1,-1,-1).contiguous().view(-1,40,50)

I don’t know if the two solutions above amount to the same thing actually…

[martinjankowiak]

looks reasonable at face value. just check on small tensors to make sure the api is doing what you want

[ffp]

Thank you so much again.

Ok, I will try and I will come back later if I need support again.

Just one “last” thing. In one of your last replies to my questions you told me to manage the case when labels y are observable and the case when they are latent separately. Right?

Then, does this imply to check if y is None and, in case is None, doing all these manipulations on shapes, otherwise not? Indeed when y is visible, there is no need for all this mess.

Anyway, just for curiosity, I tested the case when a sequential enumeration is used in place of the parallel one. All works smoothly, but is much slower. Do you advice to avoid the sequential enumeration even if the number of classes enumerated is low (e.g., 2, 3, 4)?

[martinjankowiak]

Indeed when y is visible, there is no need for all this mess.

yes that’s right

regarding enumeration that depends on your priorities, speed or code complexity. enumeration should give you a 2x speedup.