I’m trying to extend the Dirichlet process mixture model to have increasing number of clusters. I’m getting some errors in the inference stage about discrete variables so I’d like some help on how to solve them. Also I’m not really sure about the general structure of the model so some advices on that would be great!
I’ve uploaded the notebook I’m working on, and the error I’m having, to Github gist, but here is the gist of it.
I first implemented the GEM distribution to sequentially generate infinite length simplex vectors
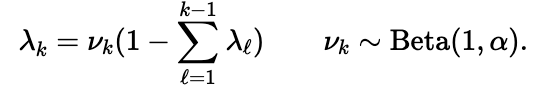
import pyro
from pyro.distributions import Beta, Normal, Gamma, Uniform
from pyro.infer import config_enumerate
import torch
import torch.tensor as T
class GEM:
rest = 1
i = 0
def __call__(self, α):
draw = pyro.sample("lambda_{}".format(self.i), Beta(1, α))
out = draw * self.rest
# print(self.i, out)
self.rest -= out
self.i += 1
return out
Because the simplex is of infinite length we can’t draw a cluster index like with the Categorical distribution; so instead we’ll draw the cluster index in an on-demand fashion: first draw a value
η from Uniform(0, 1) for each datum, the maximum value of η will then determine the number of realised clusters. We keep drawing λ from the GEM distribution till all the realised clusters are covered. that is
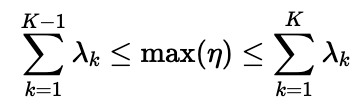
and K is the final realised number of clusters. I watched a tutorial on DP from Michael Jordan and Tamara Broderick and this is how they generate the samples.
The cluster index z for each datum is then determined by looking up the location of each η in the cumulative distribution of λ
z = torch.searchsorted(cumsum(λ), η)
(For example if we have 3 data points, first draw η=[0.45, 0.3, 0.8], then draw λ = [0.2, 0.3, 0.1, 0.15, 0.2], λ_cumsum = [0.2, 0.5, 0.6, 0.75, 0.95] and then z = [1, 1, 4]. We actually have more clusters than data points.)
Now we have the number of clusters , we can draw the emission parameters.
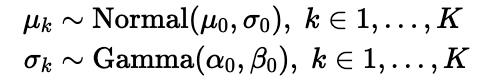
Finally the observations
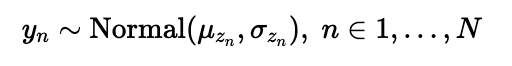
The whole model
@config_enumerate
def DPGMM(N):
"""
Dirichlet Process Gaussian Mixture Model.
N : the number of observations
"""
obs_plate = pyro.plate('n_obs', size=N)
with obs_plate:
η = pyro.sample('η', Uniform(0, 1))
total = T(0.)
G = GEM()
λs = []
while total < η.max():
λ = G(1)
total += λ
λs.append(λ)
λs = torch.stack(λs)
λs_cumsum = torch.cumsum(λs, dim=0)
z = torch.searchsorted(λs_cumsum, η)
with pyro.plate('components', len(λs)):
μ = pyro.sample('μ', Normal(0, 5))
σ = pyro.sample('σ', Gamma(3, 1))
with obs_plate:
return pyro.sample('y', Normal(μ[z], σ[z]))
I can generate samples from this model but I’m not sure what kind of effects the tensor manipulations like stack, cumsum and searchsorted have on the model and on the computational graph. When I generate some data to do inference I run into some errors
N = 100
data = torch.cat((Normal(-5, 1).sample([N*2]),
Normal(0, 0.5).sample([N]),
Normal(5, 1.5).sample([N])))
from pyro.infer.mcmc import MCMC, NUTS
kernel = NUTS(pyro.condition(DPGMM, data={'y':data}))
mcmc = MCMC(kernel, num_samples=100, warmup_steps=100)
mcmc.run(len(data))
And I got this error
RuntimeError: isDifferentiableType(variable.scalar_type()) INTERNAL ASSERT FAILED at "/Users/distiller/project/conda/conda-bld/pytorch_1595629430416/work/torch/csrc/autograd/functions/utils.h":59, please report a bug to PyTorch.
The complete error message is very long so I didn’t include it here, but it’s in the gist. Looks like I have discrete variables and HMC can’t handle them. But which one is it? Isn’t z just a generated quantity? And what am I supposed to do with it if indeed it’s it causing problems? I’m not sure how to proceed. I included config_enumerate hoping that the error will magically go away but it didn’t happen…