Implementing BNN for bimodal distribution

Misc.
1

Hi everyone,

i was reading the tutorial on BNNs implementation in pyro (Tutorial 1: Bayesian Neural Networks with Pyro — UvA DL Notebooks v1.2 documentation). In the first example, it is described how to use NUTS MCMC algorithm to sample from the posterior. Everything works ok but when I change the function and create bimodal function consisting of two sinusoids. Then my posterior predictive samples are not good.

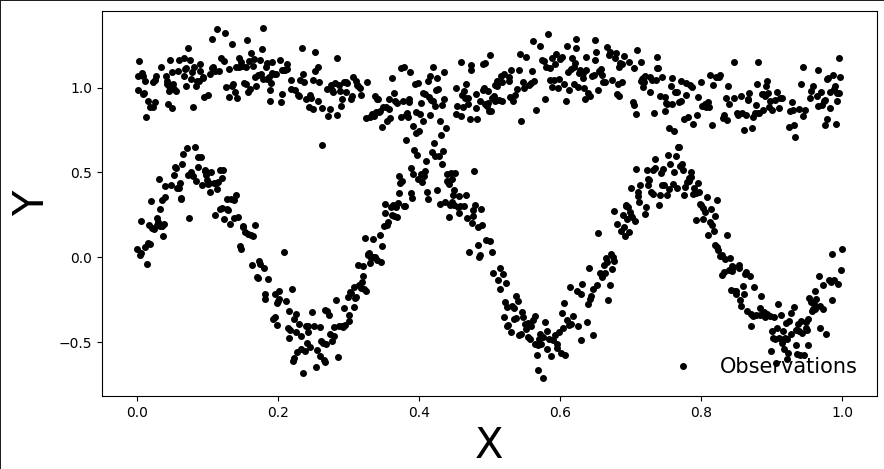
Here are the generated points of my bimodal distribution:

pic1
pic1884×469 17.7 KB

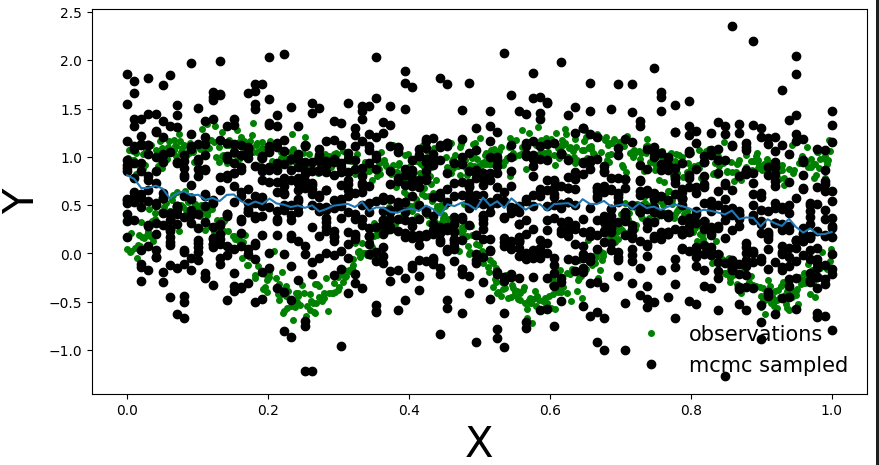
And here are the points from posterior predictive distribution. It looks that for each x the Y will be Gaussian.

pic2
pic2879×465 57.2 KB

Model is the following:

import pyro
import pyro.distributions as dist
from pyro.nn import PyroModule, PyroSample
import torch.nn as nn


class MyFirstBNN(PyroModule):
    def __init__(self, in_dim=1, out_dim=1, hid_dim=5, prior_scale=10.):
        super().__init__()

        self.activation = nn.Tanh()  # or nn.ReLU()
        self.layer1 = PyroModule[nn.Linear](in_dim, hid_dim)  # Input to hidden layer
        self.layer2 = PyroModule[nn.Linear](hid_dim, out_dim)  # Hidden to output layer

        # Set layer parameters as random variables
        self.layer1.weight = PyroSample(dist.Normal(0., prior_scale).expand([hid_dim, in_dim]).to_event(2))
        self.layer1.bias = PyroSample(dist.Normal(0., prior_scale).expand([hid_dim]).to_event(1))
        self.layer2.weight = PyroSample(dist.Normal(0., prior_scale).expand([out_dim, hid_dim]).to_event(2))
        self.layer2.bias = PyroSample(dist.Normal(0., prior_scale).expand([out_dim]).to_event(1))

    def forward(self, x, y=None):
        x = x.reshape(-1, 1)
        x = self.activation(self.layer1(x))
        mu = self.layer2(x).squeeze()
        sigma = pyro.sample("sigma", dist.Gamma(.5, 1))  # Infer the response noise

        # Sampling model
        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mu, sigma * sigma), obs=y)
        return mu

I use NUTS to sample from posterior:


model = MyFirstBNN()

nuts_kernel = NUTS(model)

mcmc = MCMC(nuts_kernel, warmup_steps=100,num_samples=300)

# Convert data to PyTorch tensors

x_train = torch.from_numpy(x_obs).float().unsqueeze(1)

y_train = torch.from_numpy(y_obs).float()

# Run MCMC

mcmc.run(x_train, y_train)

And I generate posterior predictive using the following code:

predictive = Predictive(model=model, posterior_samples=mcmc.get_samples(), return_sites=("obs", "_RETURN"))

x_test = torch.linspace(0,1, 100)

preds = predictive(x_test.unsqueeze(1))

Am I doing something wrong (too small number of samples, maybe there is some other NUTS settings) or it is just impossible to use BNN with Gaussian posterior predictive for such cases? I was reading paper Hands-on Bayesian Neural Networks – a Tutorial for Deep Learning Users
([2007.06823] Hands-on Bayesian Neural Networks -- a Tutorial for Deep Learning Users) which actually claims that it should be possible with MCMC BNN.

PS. If I add only one mode (one sinusoid instead of two), then the posterior predictive fit is good.

Thank you in advance!

Best

3

i don’t think this is something you should generically expect a bnn to do, even if you could compute the exact posterior.

note that in fitting a posterior we do not fit a predictive distribution to the data; instead we find an ensemble of neural networks each of which more or less fits the data on its own (likely under the likelihood) while being more or less likely under the prior (with different members in the ensemble appearing more/less often depending on how likely they are over all w.r.t. the joint model density).

so imagine 10% of your data comes from cos(x) and 90% comes from sin(x). sure there will be a posterior mode corresponding to cos(x) but it will contain exponentially less posterior mass than the mode near sin(x) unless you only have a handful of data points.

really you want a mixture of neural networks or some other model class: not a vanilla neural network + bayesian uncertainty.

4

so imagine 10% of your data comes from cos(x) and 90% comes from sin(x). sure there will be a posterior mode corresponding to cos(x) but it will contain exponentially less posterior mass than the mode near sin(x) unless you only have a handful of data points.

I agree and I would be satisfied if I get such result. However, it looks that my network cannot find any mode but rather considers space between sinusoids as a mode. It would be better if my network would find only one mode. This will definetly hold for SVI trained models, but I expected for MCMC BNN to be able to sample from exact posterior in my case. Also I sampled 50% points per each sinusoid so it should have same number of sampled data on each mode.

5

i don’t have much practical advice to offer as i haven’t spent much time trying to approximate bnn posteriors with mcmc. before you try anything else i’d try more samples. 100 warmup isn’t much. you might also try HMC and try tuning the step size. you might try a custom initialization using e.g. a MAP estimate (example usage of init_to_value). you might try fewer training data points: more training data points means a steeper and more difficult posterior geometry. you my try 64 bit precision (see enable_x64). you might look at other posts in this forum that do bnns. you might try software packages that are more focused on this use case like hamil torch.

6

Thanks you for suggestions. I managed to get good results by defining much larger number of samples and applying thinning on sampled posterior samples.

EDIT:

A good reference is thesis by Depeweg where similar problem was considered.

Capture
Capture728×113 26 KB

1 Like