How would you perform computations outside of sample statements while still keeping traces correct?

1

In the picture attached is a simple bayesian linear model with a Normal InverseGamma Prior. The input into the model (variable d) has the expected shape of [Batch_dim_1, …, Batch_dim_N, num_subjects, num_predictors)

In lines 87-95 there are two equivalent approaches for generating the regression parameters, but with different outcomes.

The first approach (line89-90) creates Product([Batch_dim_1, …, Batch_dim_N]) many Multivariate Normal distributions (each sampled one time - I think) with the covariance matrix properly scaled by the sampled observation noises. It works, but is greatly slowed down by the creation of all the Multivariate Normals.

The second approach (lines 93-95) creates only a single Multivariate distribution (line93/94) which is then expanded by the plates Product([Batch_dim_1, …, Batch_dim_N]) times and then sampled from. The next line (95) then provides the proper scaling with the observation noise. When running just the forward mode it is equivalent to the above approach, but when using something like poutine.trace followed by trace.compute_log_prob. The log_probabilities in the latter approach are incorrect because the “fn” is the unscaled Multivariate Normal.

Is there a way to reconcile these two approaches, keeping the speed of the latter and the correct traces of the former?

Thank you!

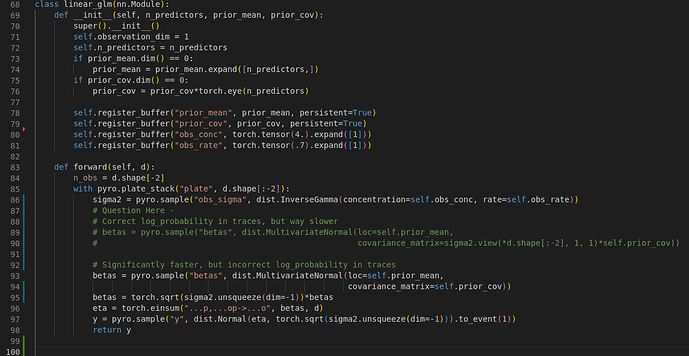
image
image1206×623 107 KB

2

Hi @Noble, these two formulations should be distributionally equivalent because they are merely different reparametrizations of the same model. IIUC you’re simply manually performing the “reparametrization trick”. There is a semantic difference in that “betas” mean different things in the first and second model, but you can record a deterministic computation “eta” in the second version such that its samples should be distributed as the samples in the first version:

  betas = pyro.sample("betas", ...)
  betas = torch.sqrt(...)
  eta = torch.einsum(...)
+ pyro.deterministic("eta", eta)
  y = pyro.sample("y", ...)

BTW it’s easy to paste code by prefixing with the line ```python and ending with the line ```. That makes it easier for readers to copy and paste snippets of your code :slightly_smiling_face:

3

Hi @fritzo, thanks for the response! I completely agree that the models are distributionally equivalent but semantically different. But I guess my question is: is it possible to make them semantically equivalent within pyro? So for a concrete example lets say we wanted to calculate the marginal prior entropy of the “beta” parameters.

import torch
import pyro
from pyro import poutine
import pyro.distributions as dist
from pyro.contrib.util import lexpand
import math

n_predictors = 5
n_subjects = 7
n_designs = 25
prior_mean = torch.zeros(n_predictors)
prior_cov = 5. * torch.eye(n_predictors)
prior_concentration = 3
prior_rate = 1

designs = torch.randn(n_designs, n_subjects, n_predictors)


def slow_linear_model_correct_traces(d):
    with pyro.plate_stack("plate", d.shape[:-2]):
        sigma2 = pyro.sample("obs_sigma", dist.InverseGamma(concentration=prior_concentration, rate=prior_rate))
        betas = pyro.sample("betas", dist.MultivariateNormal(loc=prior_mean,
                                                             covariance_matrix=sigma2.view(*d.shape[:-2], 1, 1)*prior_cov))
        eta = torch.einsum("...p,...op->...o", betas, d)
        y = pyro.sample("y", dist.Normal(eta, torch.sqrt(sigma2.unsqueeze(dim=-1))).to_event(1))
        return y

def fast_linear_model_incorrect_traces(d):
    with pyro.plate_stack("plate", d.shape[:-2]):
        sigma2 = pyro.sample("obs_sigma", dist.InverseGamma(concentration=prior_concentration, rate=prior_rate))
        betas = pyro.sample("betas", dist.MultivariateNormal(loc=prior_mean,
                                                             covariance_matrix=prior_cov))
        betas = torch.sqrt(sigma2.unsqueeze(dim=-1))*betas
        eta = torch.einsum("...p,...op->...o", betas, d)
        y = pyro.sample("y", dist.Normal(eta, torch.sqrt(sigma2.unsqueeze(dim=-1))).to_event(1))
        return y
    
def empirical_prior_entropy(model, designs):
    N = 500
    M = 50
    expanded_designs = lexpand(designs, N)
    trace = poutine.trace(model).get_trace(expanded_designs)
    
    conditoned_model = poutine.condition(model, {"betas": trace.nodes["betas"]["value"]})
    reexpanded_designs = lexpand(expanded_designs, M)
    retrace = poutine.trace(conditoned_model).get_trace(reexpanded_designs)
    retrace.compute_log_prob()
    prior_entropy = -1*(retrace.nodes["betas"]["log_prob"].logsumexp(dim=0) - math.log(M)).mean(dim=0)
    return prior_entropy

# Analytic Calculation of Prior Entropy
marginal_prior_cov = (prior_rate/prior_concentration) * prior_cov
prior_entropy = torch.distributions.StudentT(df=2*prior_concentration, loc=prior_mean, scale=torch.ones(n_predictors)).entropy().sum() \
                    + 0.5*torch.log(torch.det(marginal_prior_cov))
print(f"Analytic Prior Entropy {prior_entropy}")
# Analytic Prior Entropy 9.235673904418945

print(empirical_prior_entropy(slow_linear_model_correct_traces, designs).mean())
# Output: tensor(9.1409) - Correct
print(empirical_prior_entropy(fast_linear_model_incorrect_traces, designs).mean())
# Output tensor(11.1133) - Incorrect

We can see that the model that doesn’t reparameterize the beta parameters achieves the correct result, whereas this is not the case for the model that does reparamterize. Unfortunately there is also a significant speed difference as well.

Is it possible to keep the reparmaterization in the fast approach while still having the trace.nodes[“betas”[“log_prob”] remain correct?

Sorry about the screenshot, I’ll make sure to include the code in markdown from now on.

4

I guess you want to support conditioning on beta? In that case I’d hand-implement the forward and reverse transformations and add beta as a model arg; I know of no simpler way to do what you’re requesting.

def model(beta=None):
    ...
    transformed_beta = None
    if beta is not None:
        transformed_beta = transform.inv(beta)
    pyro.sample("transformed_beta", ..., obs=transformed_beta)
    if beta is None:
        beta = transform(transformed_beta)
    pyro.deterministic("beta", beta)
    ...

We use this design pattern in reparametrizers.

5

Yes, exactly. I’m working off of code from pyro’s EIG estimators where conditioning on parameters like beta is often necessary.

And thanks for the suggestion on using a transform, I think I know what you mean and I’ll give it a shot. Thank you for your help!