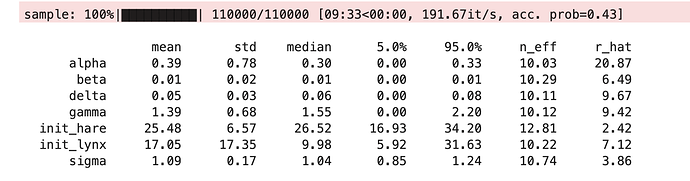
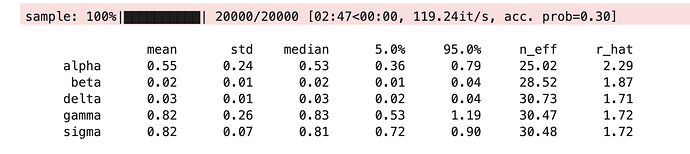
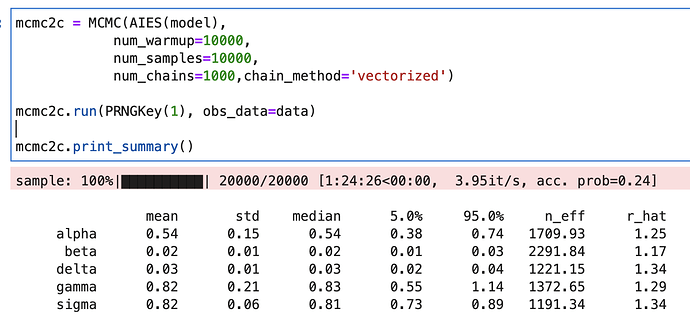
I’m new to numpyro but have used pymc and diffrax/JAX. I’m adapting the numpyro Lotka-Volterra ODE tutorial to use the JAX package diffrax that is officially recommended instead of odeint: Example: Predator-Prey Model — NumPyro documentation
Here’s my simple code rewriting that tutorial…
from jax import config
config.update("jax_enable_x64", True)
from jax.random import PRNGKey
import jax.numpy as jnp
from jax import jit
import numpyro
import numpyro.distributions as dist
from numpyro.examples.datasets import LYNXHARE, load_dataset
from numpyro.infer import MCMC, NUTS, Predictive
from diffrax import diffeqsolve, ODETerm, SaveAt, Tsit5
### download pre-packaged numpyro data for Lotka-Volterra problem
_, fetch = load_dataset(LYNXHARE, shuffle=False)
year, data = fetch() # data is in hare -> lynx order
### Lotka-Volterra ODE function
def vector_field(t, y, args):
prey, predator = y
alpha, beta, gamma, delta = args
dprey_dt = alpha * prey - beta * prey * predator
dpredator_dt = -gamma * predator + delta * prey * predator
return dprey_dt, dpredator_dt
### setup for diffrax
term = ODETerm(vector_field)
solver = Tsit5()
t0 = jnp.asarray(year[0],dtype=jnp.float64)
t1 = jnp.asarray(year[-1],dtype=jnp.float64)
dt0 = 0.1
y0 = (20,30)
args = (0.52, 0.026, 0.84, 0.026)
saveat = SaveAt(ts=jnp.asarray(year,dtype=jnp.float64)) # evaluate at same times as observations
### jitted function that solves ODE for given initial conditions (y0) and free parameters (args)
@jit
def solve_diffrax(y0,args):
# returning transposed solution so it has same dims as data: 91x2
return jnp.asarray(diffeqsolve(term, solver, t0, t1, dt0, y0, args=args, saveat=saveat).ys).T
def model(obs_data):
init_hare = numpyro.sample("init_hare", dist.LogNormal(jnp.log(10), 1)) # mean-log(10), sigma=1
init_lynx = numpyro.sample("init_lynx", dist.LogNormal(jnp.log(10), 1))
y_init = (init_hare, init_lynx)
alpha = numpyro.sample('alpha',dist.TruncatedNormal(low=0.0,loc=1.0,scale=0.5))
beta = numpyro.sample('beta',dist.TruncatedNormal(low=0.0,loc=0.05,scale=0.05))
gamma = numpyro.sample('gamma',dist.TruncatedNormal(low=0.0,loc=1.0,scale=0.5))
delta = numpyro.sample('delta',dist.TruncatedNormal(low=0.0,loc=0.05,scale=0.05))
theta = (alpha,beta,gamma,delta)
# get diffrax solution for current parameters (evaluated at same times as observations)
sol = solve_diffrax(y_init,theta)
sigma = numpyro.sample("sigma", dist.LogNormal(-1, 1).expand([2]))
numpyro.sample("y", dist.LogNormal(jnp.log(sol), sigma), obs=obs_data)
### finally do the same call as in numpyro example
###### How do I use a gradient-free (non-NUTS) approach?
mcmc = MCMC(NUTS(model, dense_mass=True),
num_warmup=1000,
num_samples=1000,
num_chains=1)
mcmc.run(PRNGKey(1), obs_data=data)
It works with NUTS but now I want to try with a gradient-free sampler for comparison. How do I change the second to last line (mcmc = MCMC(NUTS(models...))) to use a gradient-free sampler and which gradient-free samplers are recommended/available for this kind of problem?