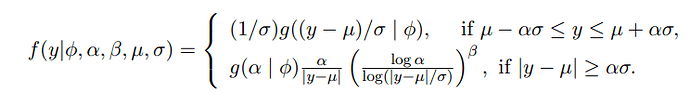I am trying to implement HMC-NUTS algorithm using a log-Pareto-tailed Normal (LPTN) distribution as my likelihood distribution. The LPTN distribution is specified as follows:
where g(.| phi) is the standard normal distribution. Note that alpha and beta are already pre-determined values so the parameters we want to make inference on are the location (mu) and scale (sigma) of the distribution.
I think I need to specify my own distribution class with some kind of truncation properties but I find it difficult because the truncation cutoff point depends on the inference parameters. Does anybody have any tips or suggestions on how to do this?
Thank you in advance.
since y has the whole real line as support i think you can just use a factor statement. something like:
numpyro.factor("my_observation", log_f_y)
where log_f_y is computed using e.g. jnp.where. is the resulting likelihood continuously differentiable?
Thank you for your reply. However, I am not sure what you exactly mean. Do you mean to use the factor statement after sampling from the distribution like this?
with numpyro.plate('data', size=len(y)):
prob = numpyro.sample('y', kpi_distribution, obs=y, rng_key=self.random_key)
numpyro.factor('prob', prob)
Unfortunately this does not change or do anything. Here, kpi_distribution denotes the LPTN distribution which I programmed myself as a custom class distribution. The main part of this class is the log_prob function which is used for the HMC-NUTS algorithm. I am almost sure that I have specified this function correctly using jnp.where etc. so I find it strange that the parameter estimates I obtain are not in line with my data generating process.
The factor replaces the sample. It is not auxiliary. Directly plug the log prob (computed however you like: a distribution is not necessary) into the factor statement