Hi All,
I have periodic timeseries data measurements (y_data). The measurements contain some noise, and the amount of noise is varying periodically.
Using simple Pytorch NN and some known input features I can get accurate point predictions (mean) of future y_data. Now, I’m trying to use Bayesian regression in Pyro to predict also the amount of noise (variance or standard deviation) in addition to the mean.
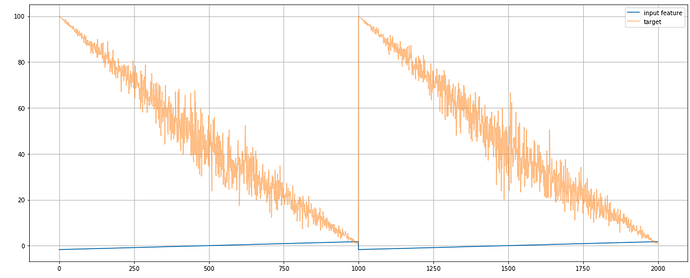
Here is an example two periods of simplified synthetic input feature (x_data) and target (y_data) I’m using to test the Pyro model:
Based on Pyro tutorials and some forum posts I have created a following model, guide, svi and prediction.
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
class SimpleTabularModel(torch.nn.Module):
def __init__(self, nx, nh, ny):
super(SimpleTabularModel, self).__init__()
self.l1 = torch.nn.Linear(nx, nh[0])
self.l2 = torch.nn.Linear(nh[0], nh[1])
self.l3 = torch.nn.Linear(nh[1], ny)
self.relu = torch.nn.ReLU(inplace=True)
self.layers = torch.nn.Sequential(self.l1, self.relu, self.l2, self.relu, self.l3)
def forward(self, x):
yhat = self.layers(x)
return yhat
nx = len(x_data[0]) # number of input features
nh = (20, 10) # size of hidden layers
ny = 1 # number of output features on last layer
N = len(train_dl.dataset) # number of training data samples
s_model = SimpleTabularModel(nx, nh, ny)
def model(x_data, y_data):
# Create unit normal priors over the parameters
priors = {}
for name, par in s_model.named_parameters():
priors[name] = dist.Normal(x_data.new_zeros(*par.shape), 1. * x_data.new_ones(*par.shape)).to_event(par.dim())
lifted_module = pyro.random_module("s_model", s_model, priors)
# sample a regressor
lifted_reg_model = lifted_module()
with pyro.plate("map", bs, subsample=x_data):
# run the regressor forward conditioned on inputs
pred_mean = lifted_reg_model(x_data)
pyro.sample("obs", dist.Normal(pred_mean, 1.).to_event(1), obs=y_data)
def guide(x_data, y_data):
dists = {}
for name, par in s_model.named_parameters():
loc = pyro.param(name + '.loc', torch.randn(*par.shape, device=device))
scale = pyro.param(name + '.scale', 1. * torch.ones(*par.shape, device=device), constraint = constraints.positive)
dists[name] = dist.Normal(loc, scale).to_event(par.dim())
# overloading the parameters in the module with random samples from the guide distributions
lifted_module = pyro.random_module("s_model", s_model, dists)
# sample a regressor
return lifted_module()
s_model.train()
lr=0.03
optim = Adam({"lr": lr})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
num_epochs = 250
pyro.clear_param_store()
pyro.enable_validation(True)
train_loss = []
for j in range(num_epochs):
epoch_loss = 0.
for x, y in train_dl:
epoch_loss += svi.step(x, y)
epoch_loss /= len(train_dl.dataset)
train_loss.append(epoch_loss)
if j % (num_epochs//10) == 0:
print("[iteration %04d] loss: %.4f" % (j, epoch_loss))
preds = []
for _ in range(100):
sampled_nn = guide(None, None)
pred_loc = sampled_nn(test_data_x)
preds.append(pred_loc.detach().numpy())
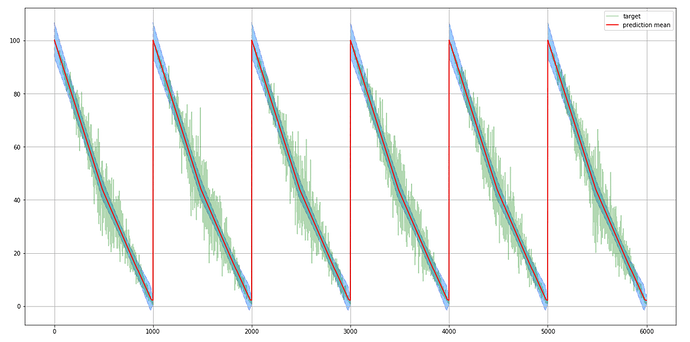
The above code is learning the mean of target, but the std of prediction (blue in the picture) doesn’t follow varying noise amplitude of the target:
I think the problem is in the following line of the model:
pyro.sample("obs", dist.Normal(pred_mean, 1.).to_event(1), obs=y_data)
, where Normal distribution is sampled always using std=1.0.
I have tried adding a sigma pyro.sample and sigma_loc pyro.param like in Bayesian Regression tutorial.
And I have also tried to add another output to NN model to get both pred_mean and pred_scale from the NN and use those in obs.
Those seemed to make SVI learning more difficult and the resulting predictions were still similar, i.e. the standard deviation of predictions did not follow the varying noise level of the target data.
How should I incorporate std or sigma to the model and guide so that the periodically varying std is learned from y_data?
And is my method of getting predictions correct?
Would it be better to use Gaussian Processes for this type of problem?
Complete Jupyter notebook can be found here:
Thanks,
Janne