How to improve sampling in case of n_eff rather low?

numpyro
1

Hi Numpyro fans,

I have a 21 parameters sampling to manage and I am using Numpyro NUTS with a model consisting of Uniform priors for same variables and Normal priors for the others, and finally the likelihood is a MultivariateNormal(signal, cov) distribution where cov is a constant covariance matrix 2250 x 2250. Now,

I use a simple running

nuts_kernel = numpyro.infer.NUTS(cond_model,
init_strategy=numpyro.infer.init_to_sample(),
max_tree_depth=5) # max_tree_depth=10

mcmc = numpyro.infer.MCMC(nuts_kernel,
num_warmup=1_000,
num_samples=8_000,
num_chains=1,
jit_model_args=True,
progress_bar=False)

The job summary indicates that r_hat is 1.00-1.01 while the n_eff for some variables are O(150) but some most are about 50 which is rather low effeiciency.

I have identified that 5 variables are highly correlated.
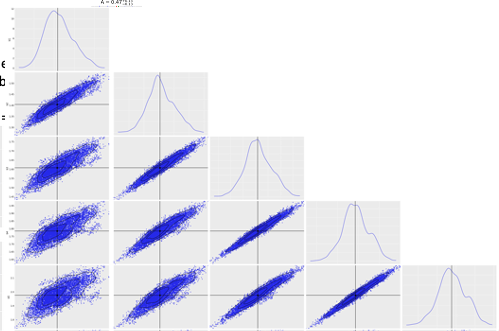
image

Do you have some advises to make the sampling more efficient? what about the mass matrix shaping for instance ?

2

I think you can try suggestions in the Bad posterior geometry and how to deal with it — NumPyro documentation tutorial.

3

Thanks @fehiepsi
o Considering for instance mass matrix structure do you think that using
dense_mass=[(“x1”,“x2”,“x3”,“x4”,“x5”)]
for the 5 correlated variables is a good starting point?
o Although using higher max_depth helps, above 5 is very demanding in my use-case.
o About SVI, does the same Numpyro model can be used ? (seems yes but I prefer to ask)

4

Yes to all. If you use SVI, it is good to start with autoguides like AutoNormal, which is ADVI in literatures.

1 Like
5

Hi @fehiepsi
Thanks for your clear advises. I just wanted

  1. if I have a

# gets some mock data
....
# compute Cov and Precision matrices : C & P
...
def model(data):
 # the priors numpyro.sample statement
....
 # compute signal 
...
 return numpyro.sample('signal', dist.MultivariateNormal(signal, 
                                                        precision_matrix=P,
                                                        covariance_matrix=C), obs=data)

Then, I have defined

guide = autoguide.AutoNormal(model)
optimizer = numpyro.optim.Adam(step_size=0.05)
svi = SVI(observed_model, guide,optimizer,loss=Trace_ELBO())
svi_result = svi.run(jax.random.PRNGKey(0), 1000, data)

Notably I was asking myself:

  1. does the guide should not be attached to the model without the observations?
  2. in the context of NUTS, the initialisation can be init_strategy=numpyro.infer.init_to_sample(), here in the context of SVI how is performed the initialisation???
  3. I have run with the above code and got rather strange behavior: negative Trace_ELBO
    => may be Trace_ELBO or AutoNormal are not ad equa and I should use AutoMultivariateNormal but then with which loss?
  4. Is there a way to get the loss evolution plot to see if there is a convergence plateau?

After playing a bit


optimizer = numpyro.optim.Adam(step_size=0.005)
guide = autoguide.AutoMultivariateNormal(model, init_loc_fn=numpyro.infer.init_to_sample())
svi = SVI(model, guide,optimizer,loss=numpyro.infer.Trace_ELBO())
svi_result = svi.run(jax.random.PRNGKey(0), 10000, data)

I get

100%|█████████████████| 10000/10000 [1:17:00<00:00,  2.16it/s, init loss: 42777.1691, avg. loss [9501-10000]: -37425.6615]

but the if I use

predictive = Predictive(guide, params=svi_result.params, num_samples=5000)
samples = predictive(jax.random.PRNGKey(1), data)

the sampling looks strange (ie gaussian like although the distrib mean a far from the truth for all variables…)

6

Look like you got most issues resolved. The remaining one is

guide = autoguide.AutoNormal(observed_model)

(Otherwise the guide will think likelihood is a latent variable).

You can plot losses using svi_result.losses.

7

Heuu, considering your remark

guide = autoguide.AutoNormal(observed_model)

I do not understand may be you refer to a pervious version of this post that I have corrected: so does the following statements are correct considering the above structure of the model function? I had a look and try to follow the AutoDAIS example but lay I am wrong

guide = autoguide.AutoNormal(model)
or
guide = autoguide.AutoMultivariateNormal(model, init_loc_fn=numpyro.infer.init_to_sample())

By the way does it makes sense to get this ELBO loss behavior during Adam optim?
image

8

Yes, it makes sense (negative loss is sometimes fine if that’s your concern, you might want to enable x64 for better numerical calculations, especially those involve Cholesky like in MVN). I modified your code by changing model to observed model (in your early code version), if that’s your question. You can see some SVI examples from those tutorials SVI Part I: An Introduction to Stochastic Variational Inference in Pyro — Pyro Tutorials 1.8.4 documentation

9

Ok thanks @fehiepsi

I had read the nice Pyro doc you point, but what is very puzzling is this

Just like the model, the guide is encoded as a stochastic function guide() that contains 
pyro.sample and pyro.param statements. 

It does not contain observed data, since the guide needs to be a properly normalized distribution.

of course it is in the Pyro-framework, and Numpyro is a little different (?) but in the case of autoguide the “guide” code is automatically generated by looking at the model provided by the user (right?). And a long this line, the model has the likelihood statement with observed data, ie. something like

return numpyro.sample('y', dist.MultivariateNormal(cl, 
                                                        precision_matrix=P,
                                                        covariance_matrix=C),
                          obs=data)

So it is why the Pyro doc is quite confusing in the context of autoguide, no?

10

Does

from jax.config import config
config.update("jax_enable_x64", True)

enable also Numpyro x64 behavior?

11

I don’t quite understand what’s your question? Are those ? are questions or just to emphasize/double check? The guide should not contain observed site, as you quoted. I guess you wanted to mention some confusing point - could you elaborate that? (Your code follows best practices but I’m not sure what’s your concern)

12

Debugging point that to AutoGuide MultiVariateNormal output an non-definite positive covariance matrix : ie. scipy eigen decomposition shows negative eigen values. The point is that scipy.linalg.cholesky based on Lapack for instance does not raise error except when lower=True argument is explicitly set.

13

Interesting, does “covariance matrix” come from the MVN guide or from the model? If it comes from the guide, could you upload your svi_result or the guide’s covariance matrix somewhere so I can enhance the guide’s parameterization? (Unless model generates nan values, the guide covariance matrix should not be non-definite) If it comes from the model, you need to address that issue (in your code that calculates the covariance matrix of the likelihood).

14

Hi @fehiepsi
It is the guide_trace['auto_scale_tril']['value']matrix. If you wish I can sent to you the svi_result that I have hopefully saved :slight_smile:

15

Sure, I think we should address that numerical issue. Thanks!

Btw, could you try to add to this line

diag = jnp.clip(diag, a_min=jnp.finfo(diag.dtype).tiny)

to see if the problem goes away?

16

Hi @fehiepsi

How do think I can proceed to this line addition? as it is part of the Numpyro library, no?

17

I think you can uninstall the current version, then install a dev version with

git clone https://github.com/pyro-ppl/numpyro.git
cd numpyro
# install jax/jaxlib first for CUDA support
pip install -e .

then you can modify the source code in numpyro folder. That would behave like you install a release version - with an additional benefit that you can modify the source code. For developing/testing, we typically use the dev version, rather than the release versions on PyPI.

18

ha ! ok I will try asap and let you know. Thanks

19

Hi @fehiepsi
I have add the line as teh following lines in class SoftplusLowerCholeskyTransform(Transform)

        diag = softplus(x[..., -n:])
        diag = jnp.clip(diag, a_min=jnp.finfo(diag.dtype).tiny) ####JEC/DU
        return z + jnp.expand_dims(diag, axis=-1) * jnp.identity(n)

Remind that with the standard Numpyro version I got

scipy.linalg.eigvalsh(cov_mtx)
array([-0.07783337, -0.06924233, -0.03830554, -0.01789377, -0.0059395 ,
        0.00183724,  0.00523341,  0.01097751,  0.01314316,  0.01835902,
        0.02327265,  0.03061616,  0.03177506,  0.04952865,  0.05483383,
        0.05734573,  0.09309918,  0.12094973,  0.15347983,  0.15643385,
        0.26808384])

Now, with the new run may be the situation is going better but still the loss behaviour is the same and more importantly the cov matrix is still Non-DP, as there is still one negative eigen-value

scipy.linalg.eigvalsh(cov_mtx)
array([-0.04128681,  0.02607654,  0.03805184,  0.0445479 ,  0.05727365,
        0.06669969,  0.073379  ,  0.07424099,  0.07551433,  0.0794809 ,
        0.08118924,  0.08282787,  0.08391205,  0.08670352,  0.09583162,
        0.10654701,  0.11219324,  0.12001006,  0.12432292,  0.1331782 ,
        0.22785095])
20

@campagne Thanks for the data! It seems that by “covariance matrix”, you are talking about the scale_tril parameter, which is the cholesky of the covariance matrix. Using your notation, what you should check is:

scipy.linalg.eigvalsh(cov_mtx @ cov_mtx.T)