How to fit models with multiple parametric families?

[mathlad]

My observation comes from N(mean, noise) where I want to model the mean as either a Relu or Sigmoid.

I want to do something like mean = q * Relu + (1-q) * Sigmoid where q comes from Bernoulli distribution. When I implemented this model, I first got the error that I need to install funsor. I did pip install funsor. After that, I got this error:

ValueError: Expected the joint log density is a scalar, but got (180,). There seems to be something wrong at the following sites: {'_pyro_dim_2'}.

None of my sample sites are named _pyro_dim_2 . 180 is the number of rows in my dataset

[martinjankowiak]

enumeration of discrete random variables can be tricky. see example code and tutorials like:

• Example: Bayesian Models of Annotation — NumPyro documentation
• Inference with Discrete Latent Variables — Pyro Tutorials 1.8.4 documentation

it is impossible to help you further if you don’t share your model code.

[mathlad]

Thanks @martinjankowiak. Let me simulate some data and get back to you with sample code

[mathlad]

@martinjankowiak here’s the code

Imports:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

import jax
import jax.numpy as jnp
from jax import random
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS

numpyro.set_platform('cpu')
numpyro.set_host_device_count(4)
numpyro.enable_x64()

seed = random.PRNGKey(0)

Data simulation:

n_subject = 2
n_segment = 3

a = jnp.array([
    [2.4, 3.2, 5.4],
    [2.53, 3.5, 5.9]
])

b = jnp.array([
    [3.4, 3.9, 3.1],
    [4.1, 3.99, 4.2]
])

n_points = 40
x = jnp.linspace(0, 10, n_points)

df = None

for i in range(n_subject):
    for j in range(n_segment):
        subject = jnp.repeat(i, n_points)
        segment = jnp.repeat(j, n_points)

        if not i and j:
            mean = jnp.minimum(jnp.maximum(
                0, b[i, j] * (x - a[i, j])
            ), 9)
        else:
            mean = jax.nn.relu(
                b[i, j] * (x - a[i, j])
            )

        y = dist.TruncatedNormal(mean, .5, low=0).sample(seed, (1,))

        if df is None:
            df = pd.DataFrame(
                jnp.array([subject, segment, x, y.reshape(-1,)]).T,
                columns=['subject', 'segment', 'x', 'y']
            )
        else:
            temp = pd.DataFrame(
                jnp.array([subject, segment, x, y.reshape(-1,)]).T,
                columns=['subject', 'segment', 'x', 'y']
            )
            df = pd.concat([df, temp], ignore_index=True).copy()

df.subject = df.subject.astype(int)
df.segment = df.segment.astype(int)

Plot simulated data:

fig, ax = plt.subplots(n_subject, n_segment, figsize=(12,6), constrained_layout=True)

for i in range(n_subject):
    for j in range(n_segment):
        sns.scatterplot(x='x', y='y', ax=ax[i][j], data=df[(df.subject == i) & (df.segment == j)])
        ax[i][j].set_ylabel('Y')
        ax[i][j].set_xlabel('X')
        ax[i][j].set_title(f'Subject {i}, Segment {j}')

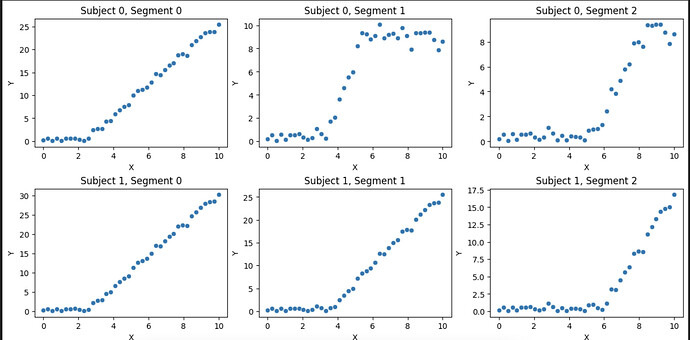
Looks like this:

As you can see, the data only saturates when subject = 0 and segment = 1, 2. So I want to fit from two parametric families: one being Relu and other being Relu that saturates (kind of like sigmoid)

Curve fitting with parametric family set to: Relu that saturates

def model(x, subject, segment, y_obs=None):
    n_subject = np.unique(subject).shape[0]
    n_segment = np.unique(segment).shape[0]

    with numpyro.plate("n_segment", n_segment, dim=-1):
        with numpyro.plate("n_subject", n_subject, dim=-2):
            a = numpyro.sample('a', dist.Normal(3, 1))
            b = numpyro.sample('b', dist.Normal(3, 1))

            c = numpyro.sample('c', dist.Normal(9, 1))

    mean = jnp.minimum(jnp.maximum(
        0, b[subject, segment] * (x - a[subject, segment])
    ), c[subject, segment])

    with numpyro.plate("data", len(x)):
        return numpyro.sample("obs", dist.TruncatedNormal(mean, .5, low=0), obs=y_obs)

x = df.x.to_numpy().reshape(-1,)
subject = df.subject.to_numpy().reshape(-1,)
segment = df.segment.to_numpy().reshape(-1,)
y = df.y.to_numpy().reshape(-1,)

# MCMC
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_chains=4, num_warmup=2000, num_samples=4000)
rng_key = jax.random.PRNGKey(0)
mcmc.run(rng_key, x, subject, segment, y)
posterior_samples = mcmc.get_samples()

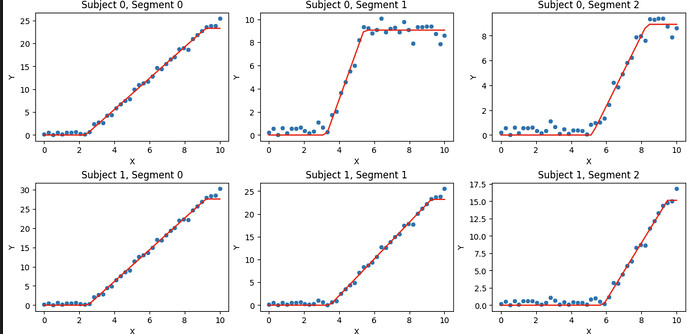
Plot results

a = posterior_samples['a'].mean(axis=0)
b = posterior_samples['b'].mean(axis=0)
c = posterior_samples['c'].mean(axis=0)

fig, ax = plt.subplots(n_subject, n_segment, figsize=(12,6), constrained_layout=True)

for i in range(n_subject):
    for j in range(n_segment):
        sns.scatterplot(x='x', y='y', ax=ax[i][j], data=df[(df.subject == i) & (df.segment == j)])
        ax[i][j].set_ylabel('Y')
        ax[i][j].set_xlabel('X')
        ax[i][j].set_title(f'Subject {i}, Segment {j}')

        mean = jnp.minimum(jnp.maximum(
            0, b[i, j] * (x - a[i, j])
        ), c[i, j])

        sns.lineplot(x=x, y=mean, ax=ax[i][j], color = 'red')

which looks like this

Now, I will change my model to fit from both the parametric families

def model(x, subject, segment, y_obs=None):
    n_subject = np.unique(subject).shape[0]
    n_segment = np.unique(segment).shape[0]

    with numpyro.plate("n_segment", n_segment, dim=-1):
        with numpyro.plate("n_subject", n_subject, dim=-2):
            a = numpyro.sample('a', dist.Normal(3, 1))
            b = numpyro.sample('b', dist.Normal(3, 1))

            c = numpyro.sample('c', dist.Normal(9, 1))

            p = numpyro.sample('p', dist.Uniform(0, 1))
            q = numpyro.sample('q', dist.Bernoulli(probs=p))

    mean = \
        q[subject, segment] * jnp.minimum(jnp.maximum(
            0, b[subject, segment] * (x - a[subject, segment])
        ), c[subject, segment]) + \
        (1 - q[subject, segment]) * jax.nn.relu(b[subject, segment] * (x - a[subject, segment]))

    with numpyro.plate("data", len(x)):
        return numpyro.sample("obs", dist.TruncatedNormal(mean, .5, low=0), obs=y_obs)

# MCMC
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_chains=4, num_warmup=2000, num_samples=4000)
rng_key = jax.random.PRNGKey(0)
mcmc.run(rng_key, x, subject, segment, y)
posterior_samples = mcmc.get_samples()

Gives the error

ValueError: Expected the joint log density is a scalar, but got (240,). There seems to be something wrong at the following sites: {'_pyro_dim_2'}.

[martinjankowiak]

what versions of jax, jaxlib, numpyro, and funsor do you have?

[mathlad]

@martinjankowiak

jax, jaxlib, numpyro, and funsor

jax==‘0.4.4’
jaxlib==‘0.4.4’
numpyro==‘0.10.1’
funsor==‘0.4.5’

edit: just updated NumPyro to 0.11.0 and jax to 0.4.5, still the same error

[martinjankowiak]

i’m not sure what’s happening. any idea @ordabayev ?

[ordabayev]

@mathlad

    mean = \
        q[subject, segment] * jnp.minimum(jnp.maximum(
            0, b[subject, segment] * (x - a[subject, segment])
        ), c[subject, segment]) + \
        (1 - q[subject, segment]) * jax.nn.relu(b[subject, segment] * (x - a[subject, segment]))

It looks like your mean has a shape of (240, 240). It should be (240,) I believe.

[mathlad]

That’s correct. There seems to be some issue with the way I’m using the Bernoulli distribution.