I want to use Pyro to design Adaptive Experiments.
In my project, I want to fit the parameters in a formula using SVI and calculate the EIG.
The formula is:
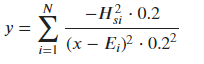
where E and Hs are parameters but Hs can be determined by E, but we do not know the exact equation, therefore I use a gp to describe this relation. My code is the following:
def model_svi(l):
ene_Mn_eg = df_Mn_eg['ene'].to_numpy()
hyb_Mn_eg = df_Mn_eg['hyb'].to_numpy()
hyb_Mn_eg_squared = hyb_Mn_eg**2
lower = np.min(ene_Mn_eg)
upper = np.max(ene_Mn_eg)
y_term = 0
x = torch.tensor(ene_Mn_eg)
with pyro.plate_stack("plate", l.shape[:-1]):
# with pyro.plate("terms", N):
E = pyro.sample("E", dist.Uniform(lower, upper))
print(E)
with torch.no_grad(), gpytorch.settings.fast_pred_var():
observed_pred = likelihood(model(E))
H_s = observed_pred.mean
for i in range(N):
y_term += (-H_s[i]**2 * 0.2) / ((x - E[i])**2 * 0.2**2)
with pyro.plate('data', len(hyb_Mn_eg_squared)):
return pyro.sample('Y_obs', dist.Normal(y_term, 0.02), obs=torch.tensor(hyb_Mn_eg_squared))
def guide(l):
with pyro.plate("terms", N):
E_loc = pyro.param("E_loc", torch.tensor(0.0))
E_scale = pyro.param("E_scale", torch.tensor(1.0), constraint=constraints.positive)
E = pyro.sample("E", dist.Normal(E_loc, E_scale))
pyro.clear_param_store()
# Set up SVI
optimizer = Adam({"lr": 0.01})
svi = SVI(model_svi, guide, optimizer, loss=Trace_ELBO())
# Training loop (you can adjust the number of steps)
num_steps = 5000
for step in range(num_steps):
loss = svi.step(x)
if step % 100 == 0:
print(f"Step {step}: Loss = {loss:.4f}")
I rewrote the code from the Pyro tutorial Designing Adaptive Experiments to Study Working Memory — Pyro Tutorials 1.9.1 documentation. But when I run the code, the error appears.
ValueError: Model and guide shapes disagree at site 'E': torch.Size([]) vs torch.Size([2])
I only started working on SVI yesterday, so I’m not very experienced with the OED. I look forward to your reply, thanks.