How to compute the uncertainty from the guide (epistemic uncertainty of BNN)?

Misc.
1

Hi all,

I am new to probabilistic programming and Bayesian inference, so I apologize in case that question is trivial or lacks clarity. I searched the forum for similar questions but couldn’t find an answer.

Let us consider a problem where we want to sample from P(Y|X,D) where X is the input, D is the training dataset, and Y is the expected output. Also, let us assume that we are using a Bayesian Neural Network (BNN) as the model, and a guide whose weights I will refer to as theta here. After inference with SVI, my understanding is that Predictive(model, guide, num_samples,...) will approximate the following integral by averaging num_samples samples of theta:

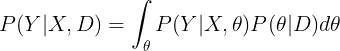margin.

Now, if I’m not mistaken, the variance of P(theta|D) can be considered as the epistemic uncertainty, and the aleatoric uncertainty is encoded in the distribution P(Y|X,theta).

However, Predictive returns samples from P(Y|X,D), and approximating the variance of those predictions (e.g. via sample variance) means that I lose the ability to distinguish between epistemic and aleatoric uncertainty.

Is there any way to recover he uncertainty from P(theta|D), which (I think) is the uncertainty of the guide? Thank you very much for your help.

Edit: After playing around, it seems that pyro.param can be used for retrieving what I’m looking for. For example, if the guide is AutoNormal, then pyro.param("AutoDiagonalNormal.scale") seems to provide what I need. However I am unsure, so confirmation of this still would be very much appreciated.

2

Hi @salehiac, you should be able to directly sample parameters from the guide. If you’re using guide = AutoNormal(model) you can draw a single sample via

one_sample = guide()

and draw a batch of samples by calling the guide inside a plate. If your model has no plates, you can

with pyro.plate("particles", 100):
    samples = guide()

if your model has a single plate you can avoid plate collision by specifying dim=-2

with pyro.plate("particles", 100, dim=-2):
    samples = guide()

If your model has more plates, just specify dim=-3 or -4 etc.

Also if you are using AutoNormal you can use the .quantiles() method, but that really only makes sense for univariate variables.

1 Like
3

Thanks a lot for your answer @fritzo. I wasn’t trying to sample from the guide though, my aim was to monitor the evolution of guide weight variances during inference to find whether I can find a simple termination criterion for the optimisation (instead of a fixed number of iterations). It probably doesn’t make much sense though.

4

Hi @salehiac, yes when I want to monitor parameters during training I typically either use pyro.param or directly access parameters of a guide module.