How do I use nested plate notation for dataset that looks like this in numpyro?

numpyro
1

How do I use nested plate notation to build a hierarchical model for dataset that looks like this:

below : intensity_i_jk, output_i_jk represent the i’th observation for (participant_j, level_k) combination

participant, level, intensity, output


participant_1, level_1, intensity_1_11, output_1_11
participant_1, level_1, intensity_2_11, output_2_11,
...
participant_1, level_1, intensity_100_11, output_100_11,

participant_1, level_5, intensity_1_15, output_1_15
participant_1, level_5, intensity_2_15, output_2_15,
...
participant_1, level_5, intensity_100_15, output_100_15,

xxx
participant_2, level_1, intensity_1_21, output_1_21
participant_2, level_1, intensity_2_21, output_2_21,
...
participant_2, level_1, intensity_100_21, output_100_21,

participant_2, level_2, intensity_1_22, output_1_22
participant_2, level_2, intensity_2_22, output_2_22,
...
participant_2, level_2, intensity_100_22, output_100_22,
participant_2, level_3, intensity_1_23, output_1_23
participant_2, level_3, intensity_2_23, output_2_23,
...
participant_2, level_3, intensity_100_23, output_100_23,
...

I have a total of 10 participants and 6 levels. For a given (participant, level) combination, I have multiple observations which vary with intensity.

The problem is – for a given participant, I have values for only some of the levels, ie, for participant_1, I have observations for only level_1 and level_5, and for participant_2 I have observations for level_1, level_2, level_3 and there are some other participants for whom I have observations for all the levels.

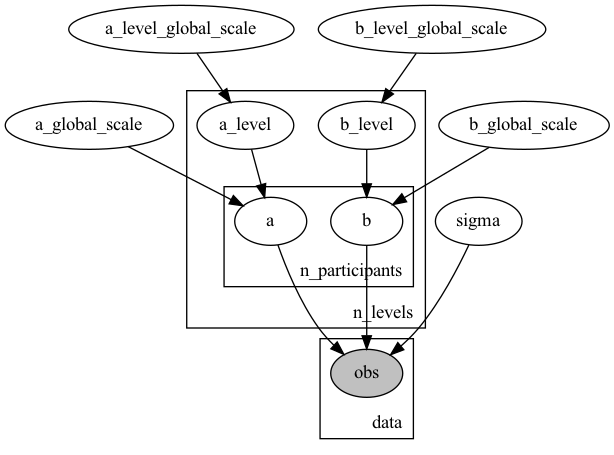
So something like this would work but it would have extra ‘unused’ parameters:

(numpyro)

    with numpyro.plate("n_levels", n_levels):
        a_level = numpyro.sample("a_level", dist.HalfNormal(a_level_global_scale))
        b_level = numpyro.sample("b_level", dist.HalfNormal(b_level_global_scale))

        with numpyro.plate("n_participants", n_participants):
            a = numpyro.sample("a", dist.Normal(a_level, a_global_scale))
            b = numpyro.sample("b", dist.Normal(b_level, b_global_scale))

This would have 10*6 parameters for a and b.

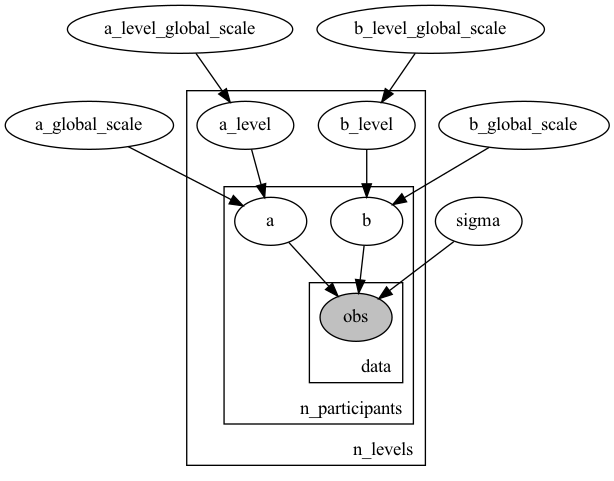
What would be the optimal way to write down the hierarchical model without the extra parameters?

Code snippets from numpyro would help.

2

@mathlad as in e.g. the CJS example, you can use numpyro.handlers.mask, which works identically to pyro.poutine.mask, to ignore missing parameters and observations in your example:

def model(data, levels_mask, observations_mask):
    ...
    with numpyro.plate("n_levels", n_levels, dim=-3):
        a_level = numpyro.sample("a_level", dist.HalfNormal(a_level_global_scale))
        b_level = numpyro.sample("b_level", dist.HalfNormal(b_level_global_scale))

        with numpyro.plate("n_participants", n_participants, dim=-2), \
                numpyro.handlers.mask(mask=levels_mask):
            a = numpyro.sample("a", dist.Normal(a_level, a_global_scale))
            b = numpyro.sample("b", dist.Normal(b_level, b_global_scale))

            with numpyro.plate("n_observations", max_n_observations, dim=-1), \
                    numpyro.handlers.mask(mask=observations_mask):
                return numpyro.sample("output", ..., obs=data)

This is statistically optimal, and while it may be wasteful computationally, if your data is not too sparse the parallelism inherent in this approach is probably worth it.

See also this forum thread for a longer and better-explained Pyro example, or search for others that use mask to encode patterns of sparsity.

1 Like
3

Hi @eb8680_2. Thank you so much for your reply. I’m quite new to numpyro, I’ll try masking after this, but could you please explain (for my understanding) what’s between these two:

Before your reply, my model was: (mep_size_obs is the output column)

def model(intensity, participant, level, mep_size_obs=None):

    a_global_scale = numpyro.sample('a_global_scale', dist.HalfCauchy(1.0))
    b_global_scale = numpyro.sample('b_global_scale', dist.HalfCauchy(1.0))

    a_level_global_scale = numpyro.sample('a_level_global_scale', dist.HalfCauchy(1.0))
    b_level_global_scale = numpyro.sample('b_level_global_scale', dist.HalfCauchy(1.0))

    n_participants = np.unique(participant).shape[0]
    n_levels = np.unique(level).shape[0]

    with numpyro.plate("n_levels", n_levels, dim=-2):
        a_level = numpyro.sample("a_level", dist.HalfNormal(a_level_global_scale))
        b_level = numpyro.sample("b_level", dist.HalfNormal(b_level_global_scale))

        with numpyro.plate("n_participants", n_participants, dim=-1):
            a = numpyro.sample("a", dist.Normal(a_level, a_global_scale))
            b = numpyro.sample("b", dist.Normal(b_level, b_global_scale))

    sigma = numpyro.sample('sigma', dist.HalfCauchy(1.0))
    mean = jax.nn.relu(b[level, participant] * (intensity - a[level, participant]))
    
    with numpyro.plate("data", len(intensity)):
        return numpyro.sample("obs", dist.TruncatedNormal(mean, sigma, low=0), obs=mep_size_obs)

The above renders as follows:

model

I tried writing my model the way you wrote above, it takes slightly more time to run MCMC on this (15 mins vs 20 mins)

def model(intensity, participant, level, mep_size_obs=None):

    a_global_scale = numpyro.sample('a_global_scale', dist.HalfCauchy(1.0))
    b_global_scale = numpyro.sample('b_global_scale', dist.HalfCauchy(1.0))

    a_level_global_scale = numpyro.sample('a_level_global_scale', dist.HalfCauchy(1.0))
    b_level_global_scale = numpyro.sample('b_level_global_scale', dist.HalfCauchy(1.0))

    n_participants = np.unique(participant).shape[0]
    n_levels = np.unique(level).shape[0]

    sigma = numpyro.sample('sigma', dist.HalfCauchy(1.0))

    with numpyro.plate("n_levels", n_levels, dim=-3):
        a_level = numpyro.sample("a_level", dist.HalfNormal(a_level_global_scale))
        b_level = numpyro.sample("b_level", dist.HalfNormal(b_level_global_scale))

        with numpyro.plate("n_participants", n_participants, dim=-2):
            a = numpyro.sample("a", dist.Normal(a_level, a_global_scale))
            b = numpyro.sample("b", dist.Normal(b_level, b_global_scale))

            mean = jax.nn.relu(b[level, participant, 0] * (intensity - a[level, participant, 0]))
    
            with numpyro.plate("data", len(intensity), dim=-1):
                return numpyro.sample("obs", dist.TruncatedNormal(mean, sigma, low=0), obs=mep_size_obs)

It renders like this:

model

I believe yours is probably the right way to write it and I’m pretty sure I’m missing something very basic. It will help me a lot if you could pin point it.

Also, wanted to clarify that in my dataset, intensity_1_11 is not same as intensity_1_21, that is, for two different (participant, level) combinations, the observations are not recorded at the same intensities. Also, the number of observations for a given (participant, level) combination is not exactly 100, this number too varies for each combination.

4

Hi @mathlad @eb8680_2
I actually want to follow up to this reply and wonder if you have an answer for that :).