Hierarchical linear regression

numpyro
1

Hello,

I try to implement a hierarchical model with numpyro based on this tutorial. I slightly modified the tutorial. I use a quadratic model instead of a linear one and generate my own data set.

My training data is generated by the the following code snippet:

import numpy as np
import pandas as pd

def simulation_data(n: int):
    res = list()
    dT = np.arange(-40, 51, 5)

    a = 1
    sigma_a = 1
    b = 2
    sigma_b = 1
    c = 0.5
    sigma_c = 1 
    
    for idx in range(n):        
        alpha0_offset = np.random.normal(0, 1)
        a0 = a + alpha0_offset * sigma_a
        alpha1_offset = np.random.normal(0, 1)   
        a1 = b + alpha1_offset * sigma_b
        alpha2_offset = np.random.normal(0, 1)   
        a2 = c + alpha2_offset * sigma_c
        
        y_true = a0 + a1 * dT + a2 * dT**2 
        sigma = np.random.exponential(1)
        
        y = np.random.normal(y_true, sigma)
        
        res.append(pd.DataFrame({'idx' : idx, 'dT' : dT, 'y' : y}))
    return pd.concat(res)

My model uses priors which are identical to the distributions above. Furthermore I use a non-centered version of the hierachical model to rule out divergences.

def model_non_centered(idx, dT, y=None):
    a = numpyro.sample("a", dist.Normal(1, 0.1))
    sigma_a = numpyro.sample("sigma_a", dist.Exponential(1))
    b = numpyro.sample("b", dist.Normal(2., 0.1))
    sigma_b = numpyro.sample("sigma_b", dist.Exponential(1))
    c = numpyro.sample("c", dist.Normal(0.5, 0.1))
    sigma_c = numpyro.sample("sigma_c", dist.Exponential(1))
    
    NUM_PARTS = len(np.unique(idx))

    with numpyro.plate("usnrs", NUM_PARTS):
        alpha0_offset = numpyro.sample("alpha0_offset", dist.Normal(0., 1.))
        alpha0 = numpyro.deterministic("alpha0", a + alpha0_offset * sigma_a)       
        alpha1_offset = numpyro.sample("alpha1_offset", dist.Normal(0., 1.))
        alpha1 = numpyro.deterministic("alpha1", b + alpha1_offset * sigma_b)                                                         
        alpha2_offset = numpyro.sample("alpha2_offset", dist.Normal(0., 1.))
        alpha2 = numpyro.deterministic("alpha2", c + alpha2_offset * sigma_c)

    mu = numpyro.deterministic("mu", alpha0[idx]  + alpha1[idx] * dT +  alpha2[idx] * dT**2)         
    eps = numpyro.sample("eps", dist.Exponential(1))
    with numpyro.plate("data", len(idx)):
        numpyro.sample("obs", dist.Normal(mu, eps), obs=y)

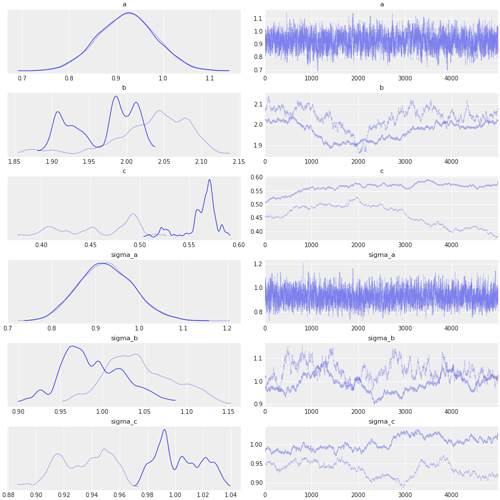
Unfortunately the model does seem to converge.

simulation = simulation_data(200)

rng_key = random.PRNGKey(1)

nuts_kernel = NUTS(model_non_centered)
non_centered_mcmc = MCMC(nuts_kernel, 
                         num_samples=5000, 
                         num_warmup=1000, 
                         num_chains=2)
non_centered_mcmc.run(rng_key, 
                      simulation.idx.values, 
                      simulation.dT.values, 
                      simulation.y.values)

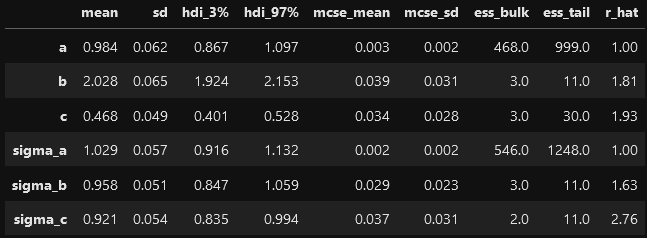
The effective sample size of e.g. b, c, sigma_b and sigma_c is very small and MCMC does not seem to explore the parameter space appropriately.

arviz
arviz864×864 152 KB

I am new to Bayesian modeling and numpyro and I am struggling to solve this issue. Can somebody please point me into the right direction?

2

in your model a etc are global random variables that are outside of the plate but in your data generating function you draw a new a sample for each iteration of the loop; these sample statements need to be moved out of the loop (note there may be other issues as well)

3

Thanks a lot for your reply. You are right. I moved the statements related to a, b, c, sigma_a, sigma_b, sigma_c outside of the for loop. I think it makes also more sense to use constants here instead of sample statements to generate the simulation data. Unfortunately the problem is still the same. The effective sample size for b, c, sigma_b, sigma_c is very low. How can I improve this?

4

this choice, which adds variable amounts of noise to each datapoint, is probably also problematic

5

I moved sigma outside the for loop and assumed a constant value of one. Unfortunately the effective sample size of b, c, sigma_b and sigma_c is still very small.

ess

Do you have another idea, what could cause this issue?

6

these tight priors may be a bad idea. e.g. you probably want something more like

a = numpyro.sample("a", dist.Normal(1, 1.0))
7

I followed your suggestion and used less tight priors for a, b, c e.g.

a = numpyro.sample("a", dist.Normal(1, 1.0))

Unfortunately the effective sample size is still very low. Could a reparametrization of the model help or is there anything else I should consider when using NUTS.

8

i believe all your issues lie in your data generative process. this is a simple model and shouldn’t be difficult to fit. you should think carefully about the form of the data you’re generating. if you generate pure noise it’s hard to fit anything sensible.

for example this choice sigma_a = 1 means that each data point will use wildly different a coefficients. more sensible would be sigma_a = sigma_b = sigma_c = 0

9

You might also want to marginalize those (might be highly correlated) offset variables. Your likelihood mu will be a + b dt + c dt2 and variance will be sigma_a2 + sigma_b2 b2 dt2 + sigmac2 c2 dt4 + eps**2. You can remove eps because it can be merged with sigma_a.