Hi all,
I’m currently developing a Hidden Markov Model (HMM) in Pyro where I’m particularly interested in modeling the transition probabilities as block diagonal matrix as discussed in The Block Diagonal Infinite Hidden Markov Model. Unlike the infinite model discussed in the paper, my model uses a finite number of blocks and states, replacing the stick-breaking priors with a Dirichlet distribution.
I’m not sure how to correctly sample from the categorical distribution to assign states to blocks and use these samples to create a mask for the block-diagonal structure, and enumerate over them. Here’s my current take (which is non-functional at the moment):
# This represents the initial probabilities of
# each block in the block diagonal matrix.
rho = pyro.sample(
"probs_rho",
dist.Dirichlet(zeta * torch.ones(blocks))
)
# Sample 'probs_x' from a Dirichlet distribution
# just like in https://pyro.ai/examples/hmm.html.
probs_x = pyro.sample(
"probs_x",
dist.Dirichlet(gamma * torch.ones(hidden_dim, hidden_dim)).to_event(1)
)
with pyro.plate('sample_blocks', hidden_dim):
# Sample the block assignment 'z'
# Assigns each state to a block
z = pyro.sample(
"z",
dist.Categorical(rho),
infer={"enumerate": "parallel"}
)
# Create a mask that identifies the blocks
# I imagine this is where things go wrong
z_matrix = z.unsqueeze(-1)
mask = z_matrix == z_matrix.T
# Adjust the transition probabilities using the mask
xi_star = 1 + xi / torch.sum(probs_x * mask, dim=1)
beta_star = pyro.deterministic(
"beta_star",
probs_x * (1 + (xi_star.unsqueeze(1) - 1) * mask.float())
)
# Finally sample the block-diagonal transition probabilities
pis = pyro.sample(
"pis",
dist.Dirichlet(alpha0 * beta_star).to_event(1)
)
I know that I’m wrong in using infer={"enumerate": "parallel"} in the context of sampling ‘z’. Can it be correctly applied here to handle discrete state enumeration. Is enumeration possible at all?
Would enumerating with a sequential plate and creating a new enumeration dimension for each assignment be a potential solution?
Any insights on whether this configuration is valid or suggestions on a better approach to enforce the block structure will be appreciated.
Thanks in advance for any help or pointers!
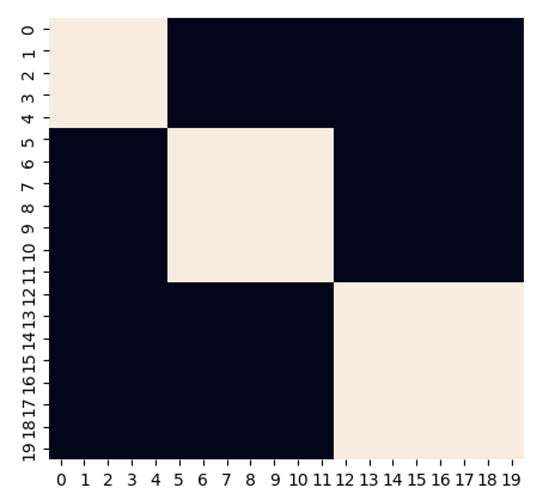
PS: As an example, for 20 states and 3 blocks, the mask matrix is:
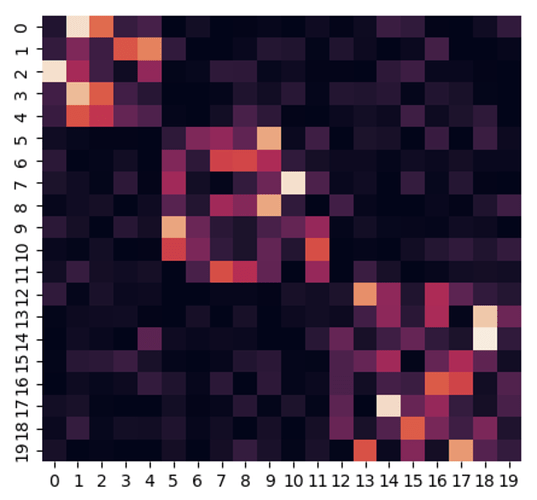
And the block-diagonal transition matrix is: