Hi there, I am working through the VAE and ssVAE tutorials (using version 1.5.1) to understand them better, but with my own data.
I have generated some synthetic regression data with a multi-linear regression equation (including quadratic and interaction effects), with 7 variables with 5 levels, thus each input is 7 floats between 0 and 1 and each has a response float between 0 and 1. The response variable is nearly normally distributed with a mean of 0.3.
To start with, I have made a regular autoencoder which achieves an RMSE of 0.15 in reconstructing the input 7 variables, see below:
class Decoder(nn.Module):
def init(self, x_dim=7,z_dim=3, hidden_dim=80):
super().init()
self.fc1 = nn.Linear(z_dim, hidden_dim)
self.fc21 = nn.Linear(hidden_dim, x_dim)
self.sigmoid = nn.Sigmoid()
self.relu = nn.ReLU()def forward(self, z): hidden = self.relu(self.fc1(z)) x = self.sigmoid(self.fc21(hidden)) return xclass Encoder(nn.Module):
def init(self, x_dim=7,z_dim=3, hidden_dim=80):
super().init()
self.fc1 = nn.Linear(x_dim, hidden_dim)
self.fc21 = nn.Linear(hidden_dim, z_dim)
self.relu = nn.ReLU()def forward(self, x): hidden = self.relu(self.fc1(x)) z = self.relu(self.fc21(hidden)) return zclass Autoencoder(nn.Module):
def init(self, x_dim=7,z_dim=3, hidden_dim=80):
super().init()
self.x_dim = x_dim
self.z_dim = z_dim
self.hidden_dim = hidden_dim
self.decoder = Decoder(self.x_dim,self.z_dim,self.hidden_dim)
self.encoder = Encoder(self.x_dim,self.z_dim,self.hidden_dim)
def forward(self,x):
z = self.encoder(x)
x_hat = self.decoder(z)
return x_hatmse = nn.MSELoss()
AE = Autoencoder(z_dim=6,hidden_dim=80)
optimizer = torch.optim.Adam(AE.parameters(),
lr = 1e-3,
weight_decay = 1e-6)
epochs=5losses =
for epoch in range(epochs):
for x,_ in train_loader:
x_hat = AE(x)
loss = mse(x,x_hat)
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(np.sqrt(loss.item()))
I have also made a regression neural network to predict the response, achieving an RMSE of 0.00, see below:
class y_predictor(nn.Module):
def __init__(self,x_dim,hidden_dim): super().__init__() self.nn = nn.Sequential(nn.Linear(x_dim,hidden_dim), nn.ReLU(), nn.Linear(hidden_dim,1), nn.Sigmoid()) def forward(self,x): return self.nn(x).squeeze(-1)NN = y_predictor(7,80)
optimizer = torch.optim.Adam(NN.parameters(),
lr = 1e-3,
weight_decay = 1e-6)
epochs=5losses =
for epoch in range(epochs):
for x,y in train_loader:
y_hat = NN(x)
loss = mse(y,y_hat)
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(np.sqrt(loss.item()))
Finally, I have attempted to setup a VAE as in the VAE tutorial, see below:
class Decoder(nn.Module):
def init(self, x_dim,z_dim, hidden_dim):
super().init()
self.fc1 = nn.Linear(z_dim, hidden_dim)
self.fc21 = nn.Linear(hidden_dim, x_dim)
self.fc22 = nn.Linear(hidden_dim, x_dim)
self.softplus = nn.Softplus()
self.sigmoid = nn.Sigmoid()def forward(self, z): hidden = self.softplus(self.fc1(z)) loc_x = self.sigmoid(self.fc21(hidden)) return loc_xclass Encoder(nn.Module):
def init(self, x_dim,z_dim, hidden_dim):
super().init()
self.fc1 = nn.Linear(x_dim, hidden_dim)
self.fc21 = nn.Linear(hidden_dim, z_dim)
self.fc22 = nn.Linear(hidden_dim, z_dim)
self.softplus = nn.Softplus()def forward(self, x): hidden = self.softplus(self.fc1(x)) z_loc = self.fc21(hidden) z_scale = torch.exp(self.fc22(hidden)) return z_loc, z_scaleclass VAE(nn.Module):
def init(self,input_dim=7,z_dim=6,hidden_dim=80):
super().init()
self.z_dim = z_dim
self.input_dim=input_dim
self.hidden_dim = hidden_dim
self.decoder = Decoder(self.input_dim,self.z_dim,self.hidden_dim)
self.encoder = Encoder(self.input_dim,self.z_dim,self.hidden_dim)def model(self, xs,ys=None): pyro.module("vae", self) with pyro.plate("data"): z_loc = xs.new_zeros(torch.Size((xs.shape[0], self.z_dim))) z_scale = xs.new_ones(torch.Size((xs.shape[0], self.z_dim))) zs = pyro.sample("z", dist.Normal(z_loc, z_scale).to_event(1)) x_loc = self.decoder(zs) pyro.sample("x", dist.Bernoulli(x_loc, validate_args=False).to_event(1), obs=xs) return x_loc def guide(self, xs,ys=None): with pyro.plate("data"): z_loc, z_scale = self.encoder(xs) pyro.sample("z", dist.Normal(z_loc, z_scale).to_event(1)) def reconstruct(self, x): z_loc, z_scale = self.encoder(x) z = dist.Normal(z_loc, z_scale).sample() x = self.decoder(z) return xlr = 1e-03
hidden_dim=80
z_dim = 6
num_epochs=5
bs = 100train_loader = DataLoader(data(X_full,y_full),batch_size=bs,num_workers=0,shuffle=True)
vae = VAE(hidden_dim=hidden_dim,z_dim=z_dim,input_dim=7)
MSE = torch.nn.MSELoss()
adam = pyro.optim.Adam({“lr”: lr})
svi = SVI(vae.model, vae.guide, adam, loss=Trace_ELBO())pyro.clear_param_store()
epoch_mse=
epoch_losses=
for epoch in tqdm(range(num_epochs),desc=‘Epochs’,unit=‘Epoch’):
epoch_loss=0.
mses =#eval for x,_ in train_loader: mse = MSE(x,vae.reconstruct(x)).item() mses.append(np.sqrt(mse)) epoch_mse.append(np.mean(np.array(mses))) #inference for x,_ in train_loader: epoch_loss+=svi.step(x) epoch_losses.append(epoch_loss/len(train_loader))
I have tried to keep neural network dimensions similar for comparability.
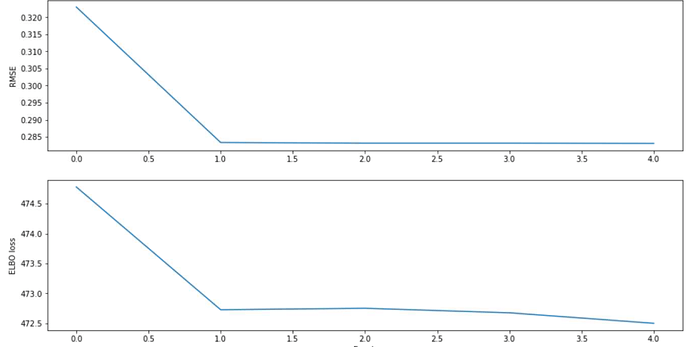
I have experimented quite a bit with varying hyper parameters for the neural networks (z-dimension, hidden-dimensions), changed activation functions, changed distribution types, optimizer parameters etc., but I keep just getting an RMSE of 0.3 for the VAE and it outputs basically 0.4 for every variable for every sample. At this point I dont know where to look for clues, I hope you could offer some insights. I hope I have supplied enough information for you to work with.
Cheers