Help with implementing Counterfactual Fairness in Pyro( Model and Guide)

Misc.
1

I’m trying to replicate the counterfactual fairness paper( https://arxiv.org/pdf/1703.06856.pdf ) in Pyro. I have found a tutorial that mentioned the following steps:

  1. Convert the above model to an SCM. Call this “GroundTruthModel”. It should explicitly represent K. In SCMs endogenous variables are deterministic functions of exogenous variables and parent endogenous variables. So sample the endogenous variables using dist.Delta.

  2. Sample synthetic data from GroundTruthModel.

  3. Create a model called “ProposedModel”. It will have the same structure as the GroundTruthModel except all the coefficients of the functional assignments of the endogenous variables and the parameters of the distributions of the exogenenous variables will be unknown parameters that are learned during training a training step. I suggest you use Greek letters for these parameters.

4)Train ProposedModel on the synthetic data using standard Pytorch/Pyro methods. Assume K is included in the training data.

5)On the trained model, use the action-abduction-inference algorithm (use both the condition operator and the do operator) to infer the counterfactual quantities of interest, namely png
Also, for the “abduction” part of the algorithm, gradient-based inference in Pyro will have problems with dist.Delta. So I suggest replacing it with PseudoDelta = partial(Normal, scale=tensor(0.1)) but using the same weights you got during training (do this conversion before training if it makes it easier).

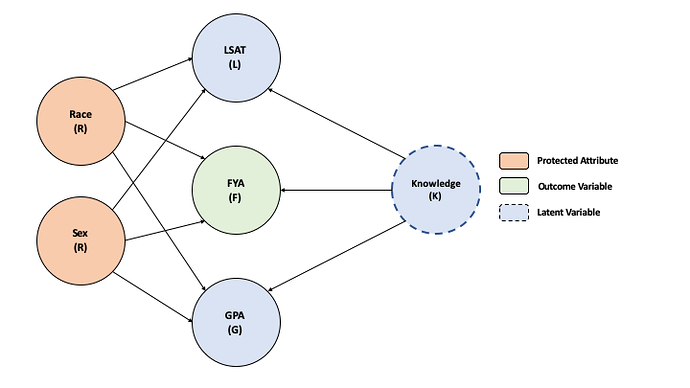
Here is my DAG:

project_dag
project_dag720×405 31 KB

Below is the code for my SCM and sampling from it (points 1 and 2)

GroundTruthModel
def GroundTruthModel():
    Nr = pyro.sample("Nr",dist.Categorical(torch.tensor([0.75,0.25]))) 
    Ns = pyro.sample("Ns",dist.Categorical(torch.tensor([0.6,0.4])))
    Nk = pyro.sample("Nk",dist.Normal(torch.tensor(0.),torch.tensor(1.))) 
    
    Nr = Nr.type(torch.FloatTensor)
    Ns = Ns.type(torch.FloatTensor)
    Nk = Nk.type(torch.FloatTensor)
   
    R     = pyro.sample("R",dist.Delta(Nr))
    S     = pyro.sample("S",dist.Delta(Ns))
    K     = pyro.sample("K",dist.Delta(Nk))
    
    
    Gval  = K + 2.1* R + 3.3 * S + 0.5 * pyro.sample("g",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    G     = pyro.sample("G",dist.Delta(Gval))
    
    Lval  = K + 5.8 * R + 0.7 * S + 0.1 * pyro.sample("l",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    L     = pyro.sample("L",dist.Delta(Lval))
    
    Fval  = K + 2.3 * R + 1.0 * S + 0.3 * pyro.sample("f",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    F     = pyro.sample("F",dist.Delta(Lval))
trace_handler = pyro.poutine.trace(GroundTruthModel)
samples = pd.DataFrame(columns=['R', 'S', 'K', 'G', 'L', 'F', 'p'])

ProposedModel

def ProposedModel():
    #Nr = pyro.sample("Nr",dist.Categorical(torch.tensor([0.75,0.25]))) 
    #Ns = pyro.sample("Ns",dist.Categorical(torch.tensor([0.6,0.4])))
    #Nk = pyro.sample("Nk",dist.Normal(torch.tensor(0.),torch.tensor(1.))) 
    
    #Nr = Nr.type(torch.FloatTensor)
    #Ns = Ns.type(torch.FloatTensor)
    #Nk = Nk.type(torch.FloatTensor)
   
    R     = pyro.sample("R",dist.Delta(chi_1))
    S     = pyro.sample("S",dist.Delta(chi_2))
    K     = pyro.sample("K",dist.Delta(chi_3))
    
    
    #Gval  = K + 2.1* R + 3.3 * S + 0.5 * pyro.sample("g",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    Gval  = K + alpha_1* R + beta_1 * S + gama_1 * pyro.sample("g",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    G     = pyro.sample("G",dist.Delta(Gval))
    
    Lval  = K + alpha_2 * R + beta_2 * S + gama_2 * pyro.sample("l",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    L     = pyro.sample("L",dist.Delta(Lval))
    
    Fval  = K + alpha_3 * R + beta_3 * S + gama_3 * pyro.sample("f",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
    F     = pyro.sample("F",dist.Delta(Lval))
trace_handler = pyro.poutine.trace(ProposedModel)
samples = pd.DataFrame(columns=['R', 'S', 'K', 'G', 'L', 'F', 'p'])

all_samples=[]
for i in range(1000):
    trace = trace_handler.get_trace()
    R = trace.nodes['R']['value']
    S = trace.nodes['S']['value']
    K = trace.nodes['K']['value']
    G = trace.nodes['G']['value']
    L = trace.nodes['L']['value']
    F = trace.nodes['F']['value']
    # get prob of each combination
    log_prob = trace.log_prob_sum()
    p = np.exp(log_prob)
    samples = samples.append({'R': R, 'S': S, 'K': K, 'G': G, 'L':L, 'F': F,'p':p}, ignore_index=True)
    all_samples.append([R,S,K,G,L,F])

samples.head()

Can someone help me understand how to work on points 3 through 5

2

Hi @TomRiddle, I recommend reading through Pyro’s introductory tutorials, especially part 1 and part 2 of the language intro and part 1 of the SVI tutorial. I’m not sure exactly what you’re having trouble with, so I’ll try to make some suggestions below about how to implement steps 3-5. Note that the more specific you can make your questions here, the more helpful we can be.

For step 3 and 4, you’ll need to declare that the parameters in ProposedModel are learnable with pyro.param:

alpha_1 = pyro.param("alpha_1", lambda: torch.tensor(1.))
...  # similarly for the other parameters
Gval  = K + alpha_1* R + beta_1 * S + gama_1 * pyro.sample("g",dist.Normal(torch.tensor(0.),torch.tensor(1.)))
...

To do inference and parameter learning, I recommend using a combination of enumeration via TraceEnum_ELBO for the discrete variables in your model and an AutoMultivariateNormal autoguide for the continuous variables:

model = pyro.infer.config_enumerate(ProposedModel)
guide = pyro.infer.autoguide.AutoMultivariateNormal(model)

For help with step 5, see these lecture notes and tutorials by @osazuwa. This tutorial seems to be a simple example of the action-abduction-inference algorithm.