Hi, I am new to pyro and wanted to infer from a GMM using SVI and relaxed categorical latent variables.
Here is my attempt:
import os
from collections import defaultdict
import torch
import numpy as np
import scipy.stats
from torch.distributions import constraints
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import pyro
import pyro.distributions as dist
from pyro import poutine
from pyro.infer.autoguide import AutoDelta
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO, config_enumerate, infer_discrete
smoke_test = "CI" in os.environ
assert pyro.__version__.startswith('1.9.1')
K = 4 # Fixed number of components.
real_assignment = torch.randint(high=K, size=(100,1))
real_scales = torch.tensor(0.1)
real_locs = torch.tensor([0,5,10,20])
data = torch.tensor(scipy.stats.norm.rvs(loc=real_locs[real_assignment], scale=real_scales))[:,0]
print("real_locs", real_locs)
print("real_scales", real_scales)
def model(i):
temperature = 0.0001 #0.1 / np.log2(i + 0.1)
weights = pyro.sample("weights", dist.Dirichlet(0.5 * torch.ones(K)))
weights[weights<1e-10] = 1e-10
scale = pyro.sample("scale", dist.Uniform(0.0, 1.0))
with pyro.plate("components", K):
locs = pyro.sample("locs", dist.Uniform(0.0, 20.0))
'''with pyro.plate("data", len(data)):
G = pyro.sample('assignment', dist.Gumbel(loc=torch.zeros(K),scale=torch.ones(K)).to_event(1))
one_hot_assignment = ((torch.log(weights) + G)/temperature).softmax(-1)
int_assignment = (one_hot_assignment*torch.arange(K).expand(len(data),-1)).sum(dim=1).int()
pyro.sample("obs", dist.Normal(locs[int_assignment], scale), obs=data)'''
with pyro.plate("data", len(data)):
one_hot_assignment = pyro.sample("assignment", dist.RelaxedOneHotCategoricalStraightThrough(temperature=torch.tensor(temperature), probs=weights))
int_assignment = (one_hot_assignment*torch.arange(K).expand(len(data),-1)).sum(dim=1).int()
pyro.sample("obs", dist.Normal(locs[int_assignment], scale), obs=data)
optim = pyro.optim.Adam({"lr": 0.1, "betas": [0.8, 0.99]})
guide = AutoDelta(
poutine.block(model, expose=["weights", "locs", "scale", 'assignment']))
# setup the inference algorithm
svi = SVI(model, guide, optim, loss=Trace_ELBO())
n_steps = 100
# do gradient steps
for i in range(1,n_steps+1):
svi.step(i)
# grab the learned variational parameters
map = guide(data)
weights = map['weights']
locs = map['locs']
scale = map['scale']
assignment = map['assignment']
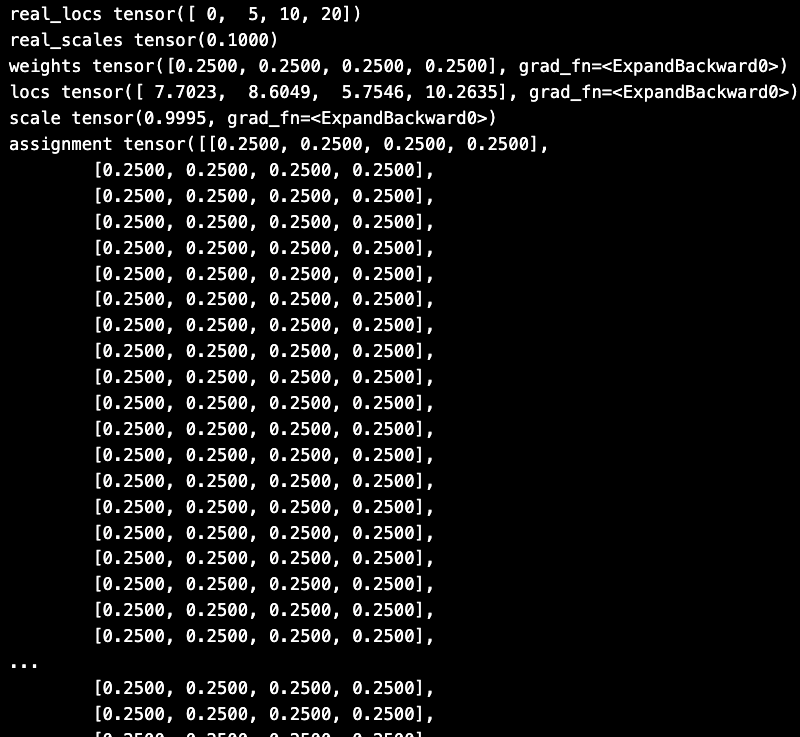
print('weights', weights)
print('locs', locs)
print('scale', scale)
print('assignment', assignment)
I tried both the pyro implementation of this article introducing the Gumbel-Softmax distribution and my own, also tried to decrease the temperature while performing svi as opposed to a fixed temperature value.
This is what the results look like :
Looks weird to me. Can someone please help me understand what is happening here ?