Hey there
So i’ve recently been doing quite a bit of work with Gaussian processes in pyro and I would appreciate your take on a few things. Essentially im trying to build a heteroscedastic Gaussian process model, and thus I need a second GP which governs the differences in variance over time. The data i’m applying it to is the following:
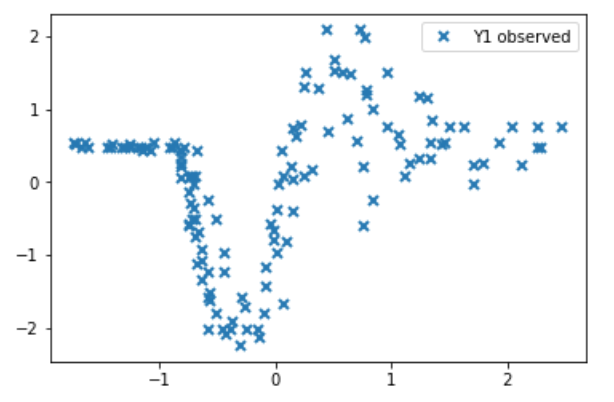
Clearly we have different noise levels over time here. The approach i’m taking is not specifically using the contributed GP modules, but is sort of derived from it. The model is seen below:
def _zero_mean_function(x):
return 0
class HGPModel(Parameterized):
def __init__(self, X, y, f_kernel, g_kernel, mean_function=None, jitter=1e-6):
super(HGPModel, self).__init__()
self.set_data(X, y)
self.f_kernel = f_kernel
self.g_kernel = g_kernel
self.mean_function = (mean_function if mean_function is not None else
_zero_mean_function)
self.jitter = jitter
def model(self):
raise NotImplementedError
def guide(self):
raise NotImplementedError
def forward(self, Xnew, full_cov=False):
raise NotImplementedError
def set_data(self, X, y=None):
if y is not None and X.size(0) != y.size(-1):
raise ValueError("Expected the number of input data points equal to the "
"number of output data points, but got {} and {}."
.format(X.size(0), y.size(-1)))
self.X = X
self.y = y
def _check_Xnew_shape(self, Xnew):
if Xnew.dim() != self.X.dim():
raise ValueError("Train data and test data should have the same "
"number of dimensions, but got {} and {}."
.format(self.X.dim(), Xnew.dim()))
if self.X.shape[1:] != Xnew.shape[1:]:
raise ValueError("Train data and test data should have the same "
"shape of features, but got {} and {}."
.format(self.X.shape[1:], Xnew.shape[1:]))
class VariationalHGP(HGPModel):
def __init__(self, X, y, f_kernel, g_kernel, likelihood, mean_function=None,
latent_shape=None, jitter=1e-6):
super(VariationalHGP, self).__init__(X, y, f_kernel, g_kernel, mean_function, jitter)
self.likelihood = likelihood
N = self.X.size(0)
def model(self, X, y=None):
N = X.size(0)
Kff = self.f_kernel(X).contiguous()
Kff.view(-1)[::N + 1] += self.jitter # add jitter to the diagonal
Lff = Kff.cholesky()
Kgg = self.g_kernel(X).contiguous()
Kgg.view(-1)[::N + 1] += self.jitter # add jitter to the diagonal
Lgg = Kgg.cholesky()
zero_loc = torch.zeros_like(X)
f = pyro.sample("f", dist.MultivariateNormal(zero_loc, scale_tril=Lff))
g = pyro.sample("g", dist.MultivariateNormal(zero_loc, scale_tril=Lgg))
if y is None:
return f
else:
return self.likelihood(f, g, y)along with the following likelihood function (just a rewritten gaussian):
class HeteroschedasticGaussian(Likelihood):
def __init__(self, variance=None):
super(HeteroschedasticGaussian, self).__init__()
def forward(self, f, g, y=None):
y_dist = dist.Normal(f, torch.exp(g))
if y is not None:
y_dist = y_dist.expand_by(y.shape[:-f.dim()]).to_event(y.dim())
return pyro.sample("y", y_dist, obs=y)Im currently using an autoguide, namely the AutoMultivariateNormal and the results i’m getting seems to be very noisy, when comparing to the pyro.contrib.gp (for non heteroscedastic cases). Inference is done using the SVI class, so im using the samples as done in many of the other pyro tutorials, as well as using the Predictive class.
pyro.clear_param_store()
f_rbf = gp.kernels.RBF(input_dim=1, lengthscale=torch.tensor(1.), variance=torch.tensor(1.))
g_rbf = gp.kernels.RBF(input_dim=1, lengthscale=torch.tensor(1.), variance=torch.tensor(1.))
like = HeteroschedasticGaussian()
sgphetcens = VariationalHGP(X=X1, y=Y1, f_kernel=f_rbf, g_kernel=g_rbf, likelihood=like, jitter=1e-03)
guide = AutoMultivariateNormal(sgphetcens.model)
optimizer = pyro.optim.ClippedAdam({"lr": 0.003,"lrd": 0.99969})
svi = SVI(sgphetcens.model, guide, optimizer, Trace_ELBO(num_particles=1))
num_epochs = 5000
losses = []
pyro.clear_param_store()
for epoch in range(num_epochs):
loss = svi.step(X1, Y1)
losses.append(loss)
if epoch%100 == 99 or epoch == 0:
predictive = Predictive(sgphetcens.model, guide=guide, num_samples=1000,
return_sites=("f", "g", "_RETURN"))
samples = predictive(X1)
f_samples = samples["f"]
g_samples = samples["g"]My problem is then that the outputs, both in terms of “f” and “g” are very noisy. Generally it seems that a problem arises between the amount of jitter added to the diagonal and the number of elbo samples. Initially, the matrix becomes singular with a very low jitter term, thus resulting in errors in the cholesky factorization. Increasing it seems to fix this issue, however the model has a hard time learning anything, meaning that I have to increase it even more. This produces the noisy (and very spikey) estimates.
Through much experimentation I found that there seems to be a “sweet spot” between the amount of jitter and the number of elbo samples, which eventually produces much smoother estimates. I’m just wondering why this is the case, and why this is not particularly a problem for the contributed pyro modules?
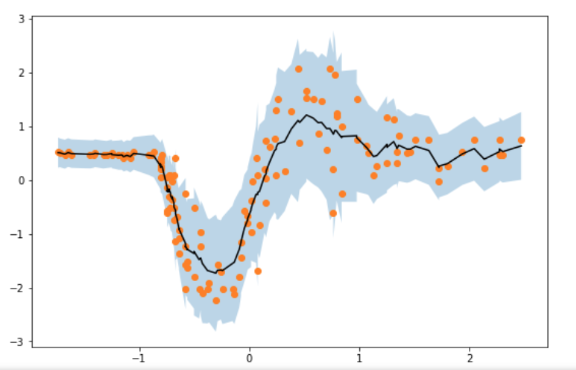
The below image shows the spikey estimates