Hi all,
I have a model which first I implemented in numpyro and then in pymc.
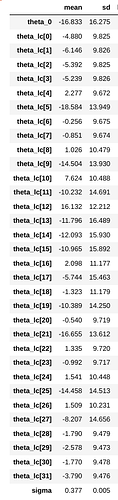
I ran the inference with NUTS sampling for both implementation and I get much higher standard deviations in theta parameters from numpyro inference. The model itself is very simple. I have also included the summary for infer results. I think I have issue with shapes or in jnp.einsum .
For both implementations I used 2000 draws with 1000 tuning steps and target_accept = 0.99. The mean posterior prediction on observation are quite similar on both.
I will appreciate if anyone can help.
C = 4
L = 8
x.shape = (2400,32)
Numpro model
def additive_model(L: int = None,
C: int = None,
x: DeviceArray = None,
y: DeviceArray = None) -> DeviceArray:
# Additive GP map: phi = theta_0 + dot(x, theta_lc)
## GP map parameters
theta_0 = numpyro.sample('theta_0', dist.Normal(loc=0, scale=20))
theta_lc = numpyro.sample('theta_lc',
dist.Normal(loc=jnp.zeros((L*C)),
scale=20*jnp.ones((L*C))))
latent_val = theta_0 + jnp.einsum('i,ji->j',theta_lc,x)
phi = numpyro.deterministic('phi', latent_val)
# Pre-defined measurement process: log(1+e^\phi)
g = jnp.log(1+jnp.exp(phi))
# Noise model
sigma = numpyro.sample('sigma', dist.HalfNormal(scale=1))
return numpyro.sample('yhat', dist.Normal(loc=g, scale=sigma), obs=y)
Pymc model
additive_model = pm.Model()
with additive_model:
# Additive GP map: phi = theta_0 + theta_lc*x
## GP map parameters
theta_0 = pm.Normal('theta_0', mu=0, sigma=20)
theta_lc = pm.Normal('theta_lc', mu=0, sigma=20, shape=(L*C))
## Latent phenotype
latent_val = theta_0 + np.einsum('i,ji->j',theta_lc,x)
phi = pm.Deterministic('phi', latent_val)
# Pre-defined measurement process: log(1+e^\phi)
g = np.log(1+np.exp(phi))
# Noise model
sigma = pm.HalfNormal('sigma', sigma=1)
Y_hat= pm.Normal('yhat', mu = g, sigma = sigma, observed=y)