Hello,
I have a simple model where the center of a normal is picked by another normal.
The following code defines a model, a guide, a data generation function, then samples from the data, uses it to infer the variables, substitutes the variables in and then plots both the original data, and the inferred distribution.
import jax.numpy as jnp
import numpyro as npy
from arviz import InferenceData
from jax import lax, random
import arviz
from matplotlib import pyplot as plt
from numpyro import handlers
from numpyro.distributions import *
def model():
with npy.plate("observations", len(data)):
c_dist = Normal(0.0, 1.0)
center = npy.sample("center", c_dist)
npy.sample(f"result", Normal(center, 1.0), obs=data)
def guide():
npy.sample(
"center",
Normal(
npy.param("a", 0.0), npy.param("b", 1.0, constraint=constraints.positive)
),
)
def test_data(a, b):
return Normal(npy.sample("center", Normal(a, b)), 1.0)
with handlers.seed(rng_seed=random.PRNGKey(0)):
data = []
for i in range(10000):
data.append(npy.sample("data", test_data(3, 3)))
data = jnp.array(data).flatten()
optimizer = npy.optim.Adam(step_size=0.1)
svi = npy.infer.SVI(
model=model,
guide=guide,
optim=optimizer,
loss=npy.infer.Trace_ELBO(),
)
init_state = svi.init(random.PRNGKey(0))
state, losses = lax.scan(
lambda state, i: svi.update(state), init_state, jnp.arange(10000)
)
results = svi.get_params(state)
for k, v in results.items():
if jnp.isnan(v):
print(k, "is nan", v)
else:
print(k, v)
count = 0
print(losses[-1])
with handlers.seed(rng_seed=random.PRNGKey(0)):
predicted = []
for i in range(10000):
predicted.append(npy.sample("pred", test_data(results["a"], results["b"])))
predicted = jnp.array(predicted).flatten()
arviz.plot_dist(data, label="Ground truth")
arviz.plot_dist(predicted, label="Predicted", color="red")
plt.show()
Here is the plot produced by the aforementioned code:
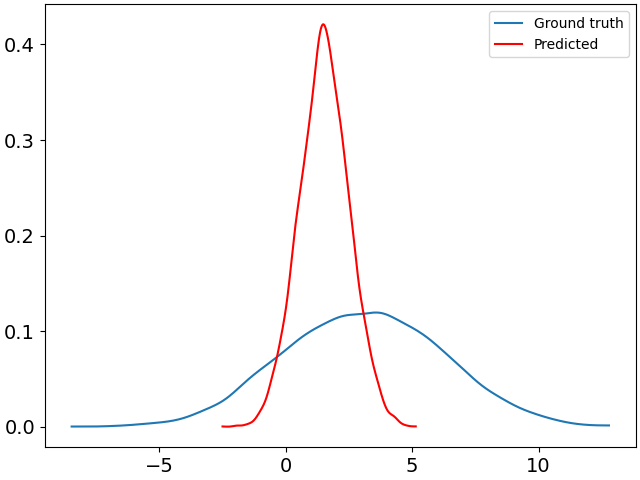
They don’t really match. Is there something I’m missing?
In addition, is there a way to sample a large amount of points at once from a function such as test_data? Of note is that calling methods on the generated distribution object wouldn’t really work, because the “center” parameter would be sampled only once.
Thanks