Example Kernel: Metropolis

numpyro
1

I’m learning numpyro and to build my skills I’m trying to implement a Metropolis Kernel that uses a model instead of a potential.

I’ve cobbled something together that seems to work, at least on simple examples, and I’m looking for feedback about how to do this more robustly and more in the NumPyro style. Is there documentation I have missed about kernel coding that you can point me to? Any feedback is welcome!

Here is the sample method of my kernel class:

def sample(self, state, model_args, model_kwargs):
    rng_key, key_proposal, key_accept = random.split(state.rng_key, 3)

    z_flat, unravel_fn = ravel_pytree(state.z)
    z_proposal = dist.Normal(z_flat, self._step_size).sample(key_proposal)
    z_proposal_dict = unravel_fn(z_proposal)
    
    log_pr_0, model_tr_0 = util.log_density(self._model, model_args, model_kwargs, state.z)
    log_pr_1, model_tr_1 = util.log_density(self._model, model_args, model_kwargs, z_proposal_dict)
    accept_prob = jnp.exp(log_pr_1 - log_pr_0)
    z_new = jnp.where(dist.Uniform().sample(key_accept) < accept_prob, z_proposal, z_flat)
    
    return MetState(unravel_fn(z_new), rng_key)

I’ve put the full code for the class and a self-contained example run in this gist so that it has line numbers and revision control.

2

Hi @abie, the code looks great. You might want to extend the code to make it work for models with "constrained-support latent variables (e.g. those with LogNormal). For that, you can use the initialize_model utility similar to here to convert model to potential_fn together with postprocess_fn.

3

Thanks for this tip, it helped me identify a surprising defect in my implementation. When I first tested with a Normal distribution, things looked plausible:

def model():
    numpyro.sample('x', dist.Normal(0,1))

kernel = Metropolis(model, step_size=.1)
mcmc = MCMC(kernel, num_warmup=0, num_samples=500_000, thinning=500)
mcmc.run(rng_key, init_params={'x':0.0})
posterior_samples = mcmc.get_samples()
plt.hist(posterior_samples['x'], bins=50)

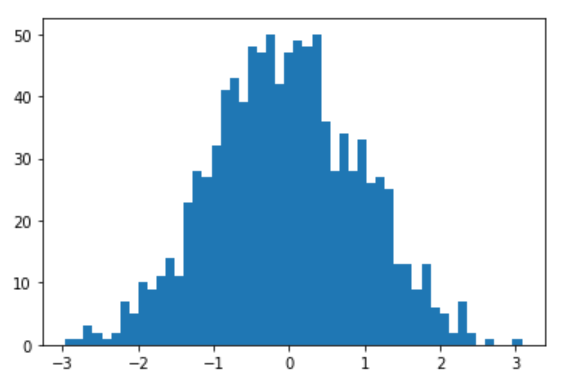
image

But when I tried with a simple constrained distribution instead (Uniform), things are clearly not right:

def model():
    x = numpyro.sample('x', dist.Uniform(0,1))

kernel = Metropolis(model, step_size=.1)
mcmc = MCMC(kernel, num_warmup=0, num_samples=500_000, thinning=500)
mcmc.run(rng_key, init_params={'x':0.0})
posterior_samples = mcmc.get_samples()
plt.hist(posterior_samples['x'], bins=50)

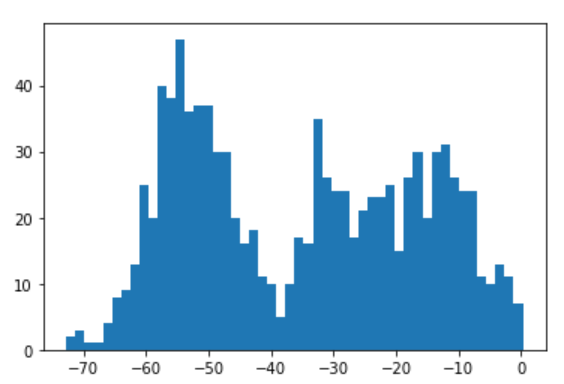
image
(Note that these samples are not constrained to the interval [0,1].)

I followed the example code you pointed me to and got something that stays within the Uniform’s support. It ended up needing a lot more code in the init method than my first attempt, though. Am I over-complicating things? Again any feedback is welcome!

class Metropolis(MCMCKernel):
    def __init__(self, model, step_size=0.1):
        self._model = model
        self._step_size = step_size
        
    @property
    def sample_field(self):
        return "z"

    @property
    def default_fields(self):
        return ("z",)
        
    def init(self, rng_key, num_warmup, init_params, model_args, model_kwargs):
        assert rng_key.ndim == 1, "only non-vectorized, for now"
        init_params_2, potential_fn, postprocess_fn, model_trace = util.initialize_model(
            rng_key,
            self._model,
#             init_strategy=self._init_strategy,
            dynamic_args=True,
            model_args=model_args,
            model_kwargs=model_kwargs,
        )
        self._potential_fn = potential_fn
        self._postprocess_fn = postprocess_fn
        
        _, unravel_fn = ravel_pytree(init_params)
        def _make_log_prob_fn(potential_fn, unravel_fn):
            def log_prob_fn(x):
                return -potential_fn(unravel_fn(x))
            return log_prob_fn
        self._log_prob_fn = _make_log_prob_fn(
            potential_fn(*model_args, **model_kwargs), unravel_fn
        )

        return MetState(init_params_2.z, rng_key)
    
    def postprocess_fn(self, args, kwargs):
        if self._postprocess_fn is None:
            return identity
        return self._postprocess_fn(*args, **kwargs)

    def sample(self, state, model_args, model_kwargs):
        rng_key, key_proposal, key_accept = random.split(state.rng_key, 3)

        z_flat, unravel_fn = ravel_pytree(state.z)
        z_proposal = dist.Normal(z_flat, self._step_size).sample(key_proposal)
        z_proposal_dict = unravel_fn(z_proposal)
        
        log_pr_0 = self._log_prob_fn(z_flat)
        log_pr_1 = self._log_prob_fn(z_proposal)
        accept_prob = jnp.exp(log_pr_1 - log_pr_0)
        z_new = jnp.where(dist.Uniform().sample(key_accept) < accept_prob, z_proposal, z_flat)
        
        return MetState(unravel_fn(z_new), rng_key)

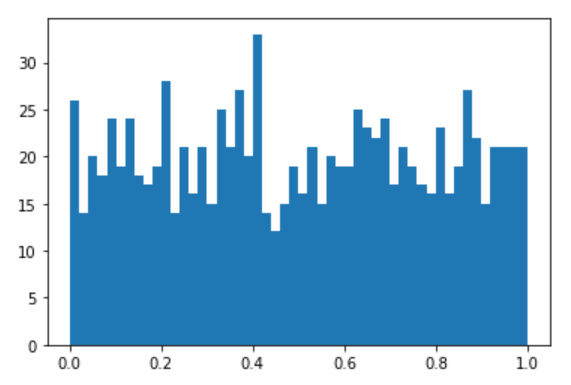
image

I’ve put the code for the class and a self-contained example run in this gist so that it has line numbers and revision control.

4

The code looks great to me. Somethings like

        if self._postprocess_fn is None:
            return identity

    @property
    def default_fields(self):
        return ("z",)

or logics around unravel_fn can be cleaned up.

needing a lot more code in the init method

I’m not sure if we can simplify this. I’m seeing you are adding 4-5 statements in the init method

init_params_2, potential_fn, postprocess_fn, model_trace = ...
z_flat, unravel_fn = ravel_pytree(init_params_2.z)
self._log_prob_fn = lambda x: -potential_fn(*model_args, **model_kwargs)(unravel_fn(x))
self._postprocess_fn = postprocess_fn
return MetState(init_params_2.z, rng_key)

Maybe you can adjust it a bit to make the sample method simpler (no need for unravel_fn logic)?

...
self._postprocess_fn = lambda x: postprocess_fn(unravel_fn(x))
return MetState(z_flat, rng_key)
5

I think i see what you mean. I’ve updated the code in the gist to keep all the unraveling in the init method and that makes things cleaner. Thanks!

I’m still confused about where I need to use the model_args and model_kwargs; it seems like they are not necessary in my postprocess and sample methods, as I have coded them. I’m sure I am missing something, though. Can anyone help me understand what?

6

It depends on dynamic_args=True or False (see docstring). If it is True, the initialize_model utility will return pairs of potential_fn_generator and postprocess_fn_generator such that potential_fn_generator(*args, **kwargs), postprocess_fn_generator(*args, **kwargs) will be the potential function and postprocess function respectively. This is useful when you want to perform MCMC.run repeatedly for different model arguments (to reduce overhead of initializing steps for later runs). I don’t think you’ll need to worry about it. It is better to set dynamic_args=False and forget about those model_args/kwargs.

7

Helpful, thanks again! I agree, it is simpler and clearer with dynamic_args=False. For anyone who wants to see the change, I’ve updated the gist.