Estimating a discontinuous parameter (angle)

Misc.
1

Hello,

I am implementing a dynamical model that transitions from state to state using a transition matrix F. So the transition model would look like x_t = F* x_(t-1).
One of my state variables is an angle that is defined as \theta = arctan2(y,x). This angle is discontinuous, so it jumps from pi to -pi at y=0, x<0. I am wondering if it is possible to estimate this discontinuous angle in Pyro?

Right now my model in Pyro looks like this:

def model(prior, cov0, data, F):
    for t in range(len(data)):
        # Transition model formula
        state = pyro.sample("state_{}".format(t), dist.MultivariateNormal(prior,cov0))
    
        # Nonlinearity function h(x_t)
        c_state = rod_observer_1(state)
    
        # Observation model formula
        pyro.sample("measurement_{}".format(t), dist.MultivariateNormal(c_state, cov1), obs = data[t])
        prior = F@state.T

My transition model looks like this
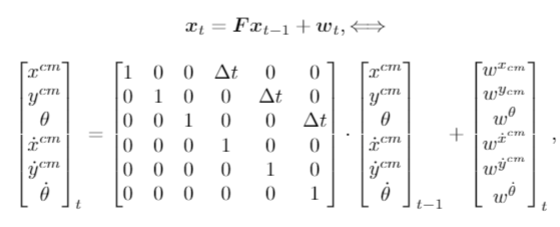
image

Pyro is able to estimate the position and their velocity state parameters well, but is not able to estimate the jump from pi to - pi , when crossing the y axis. So the real angle (theta) goes from roughly pi to -pi in a single time step, but the estimated pyro parameter angle goes gradually from pi to -pi in several time steps.

Is it possible to estimate this discontinuous angle as a parameter in Pyro?
And if so, how?

2

Hi @angelique,
I would recommend changing coordinates by embedding your angle in a 2-d space, then treating the radius as a nuisance parameter. It looks like you’re already parametrizing in terms of (x,y), so I would try to get Pyro to estimate the joint posterior over those, and only compute arctan2(y,x) after drawing posterior samples.

3

Thank you. The reason I wanted to incorporate the angle is because when I take a look at more difficult models this angle might be neccesary. I solved this particular instance without the angle, but I am still wondering if it would be possible to estimate a discontinuous angle parameter in Pyro.

4

One way Pyro can infer angles in Pyro is to use ProjectedNormal distributions together with a ProjectedNormalReparam reparametrizer that behind the scenes embeds the angle in higher-dimensional euclidean space, but this way still represents angles as pairs (x,y) on the unit circle. You might also check out the circular constraint in NumPyro. I believe @OlaRonning and @fehiepsi have thought about inference of wrapped circular variables.