Hey guys - I was curious if there is a way to, like random “mean” effects - which the 8 school example is - to do random “volatility” effects. You would think this is possible, but it turns out there are issues. For example, consider a model like like this (think of this as pseudo-code - I didn’t actually test this, so there are likely issues) - n_i is the number of observations for the i’th school:
def eight_schools(J, sigma, y=None):
mu = numpyro.sample('mu', dist.Normal(0, 5))
tau = numpyro.sample('tau', dist.HalfCauchy(5))
sigma_prior_mean = numpyro.sample('sigma_prior_mean ', dist.Normal(0, 10))
sigma_prior_scale = numpyro.sample('sigma_prior_mean ', dist.HalfNormal(0, 20))
with numpyro.plate('J', J):
sigma_i = numpyro.sample('sigma_prior',dist.LogNormal(sigma_prior_mean, sigma_prior_scale))
theta = numpyro.sample('theta', dist.Normal(mu, tau))
numpyro.sample('obs', dist.Normal(theta, sigma_i/sqrt(n_i), obs=y)
You might imagine something like this works. However, it is well-known that the maximum likelihood estimator for the variance of a normal distribution is biased - specifically, the MLE estimator is:
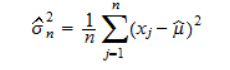
Consider what happens when you have groups with a small number of estimations. The MLE estimator is heavily biased towards 0 (indeed, when you have 1 observation in the group, the MLE estimator for the variance is 0). This issue causes one to get unrealistic results, at least when the number of samples per group is small, since instead of the volatility estimate being shrunk towards to unconditional volatility mean, it’s shrunk heavily towards 0.
Is there a way to correct for this issue, and hence allow for a random volatility to work? Hopefully this question makes sense.