So what I love about pyro is the ability to marginalize out discrete variables (when using for example NUTS). However, I can’t get it in the specific format I am interested in… This is the model structure:
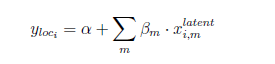
![]()
I have for each individual m latent variables, the mean of this latent variable can vary across individuals and is known. The latent variables are assumed to be Poisson distributed. I know enumeration is not possible for the Poisson variable as the distribution is unbounded. Yet for research purposes, I would like to stick to NUTS and thus I need to find a way how I could still implement this structure. My first instinct was to convert the Poisson to dist.categorical and thus disregard the extreme values that have a low probability and re-scale the other probabilities such that it still sums up to one.
Unfortunately, I got an error about tensor shapes so I added shapes. Below you can find a simplified version of my model. The model below runs however for each individual it now has the same mean and it is seen as a prior rather than a known constant (I think?). (Normally p_poisson known as gamma in the equation is calculated before model_pyro_forum_pyro is calculated).
So how could I achieve this? and is it possible to do parallel enumeration in this case?
def model_pyro_forum_pyro(x_latent_mean, y):
n = x_latent_mean.shape[0]
m = x_latent_mean.shape[1]
max_extreme_value = 15
a = np.zeros(shape=(max_extreme_value, n, m))
for i in range(0, max_extreme_value):
a[i, :, :] = poisson.pmf(i, x_latent_mean)
a = a.transpose(1,2,0)
p_poisson = Variable(torch.Tensor(a))
alpha = pyro.sample('alpha', dist.Normal(0.0, 1.0))
with pyro.plate('latent_value', m):
latent_coef = pyro.sample('latent_coef',
dist.Normal(0.0, 0.25))
with pyro.plate('data'):
x_latent = pyro.sample(f"x_latent", dist.Categorical(p_poisson[0, :, :]),
infer={"enumerate": "sequential"})
y_loc = alpha + (x_latent * latent_coef).sum(dim=-1)
pyro.sample('y', dist.Bernoulli(logits=y_loc), obs=y)