I am still getting the hang of Pyro and SVI in general, and in particular, looking at inference with discrete latent variables. I spent some time on exploring enumeration [1-2], but was really struggling to grasp the dimensionality of enumerated variables. In particular, I was struggling in reading [2] to understand how I would know what to set as first_available_dim. However, @martinjankowiak’s dire comment at [3] largely put me off of this approach. Specifically:
unfortunately for all practical purposes i think it’s essentially impossible to get SVI to work in these kinds of models, especially if you want to push to large
p
So I am looking at a relaxed Bernoulli [4]. My biggest question is simply if I am missing something, as this seems to work too well. The model:
import os
import torch
from torch.distributions import constraints
import numpy as np
import pandas as pd
import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO, Predictive, TraceEnum_ELBO, config_enumerate, infer_discrete
def model(predictors, h_pred, pheno):
n_predictors = predictors.shape[1]
gamma_0 = pyro.sample("g0", dist.Normal(0., 1.))
covs = pyro.sample("covs", dist.Normal(torch.zeros(n_predictors), torch.ones(n_predictors)).to_event(1))
pi = pyro.sample("pi", dist.Beta(2., 2.))
z = pyro.sample("z", dist.RelaxedBernoulliStraightThrough(torch.tensor(1.0), probs=pi))
l = (gamma_0 + torch.matmul(predictors, covs.squeeze()) + h_pred * z).squeeze(-1)
with pyro.plate("pheno", predictors.shape[0]):
p = pyro.sample("obs", dist.Bernoulli(logits=l), obs=pheno)
return z,pi
def guide(predictors, h_pred, pheno):
n_predictors = predictors.shape[1]
g0_loc = pyro.param("g0_loc", torch.tensor(0.))
g0_scale = pyro.param("g0_scale", torch.tensor(1.), constraint=constraints.positive)
gamma_0 = pyro.sample("g0", dist.Normal(g0_loc, g0_scale))
covs_loc = pyro.param("covs_loc", torch.zeros(n_predictors))
covs = pyro.sample("covs", dist.Normal(covs_loc, 1.).independent(1))
alpha = pyro.param("alpha", torch.tensor(2.), constraint=constraints.positive)
beta = pyro.param("beta", torch.tensor(2.), constraint=constraints.positive)
pi = pyro.sample("pi", dist.Beta(alpha, beta))
z = pyro.sample("z", dist.RelaxedBernoulliStraightThrough(temperature=torch.tensor(1.0), probs=pi))
l = (gamma_0 + torch.matmul(predictors, covs.squeeze()) + h_pred * z).squeeze(-1)
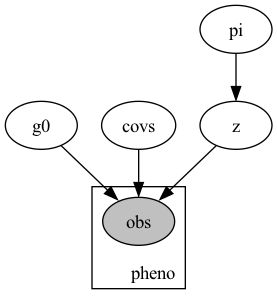
So Z is a latent Bernoulli variable governed by parameter pi. Near as I can tell, I get sensible results from directly deploying the relaxed Bernoulli as if I had been working with a un-relaxed one:
torch.manual_seed(1)
predictors = torch.rand([100, 3])
coefs = torch.tensor([1., -5, 0.2])
hidden_feat = np.zeros(100)
hidden_feat[51:] = 5 ## i.e. hidden_feat has a large impact on the outcome variable
hidden_feat = torch.tensor(hidden_feat)
pheno = torch.bernoulli(torch.sigmoid(0.2 + torch.matmul(predictors, coefs) + hidden_feat))
pyro.clear_param_store()
num_steps = 10000
lr0 = 0.01
gamma = 0.1
lrd = gamma ** (1/num_steps)
optim = pyro.optim.ClippedAdam({'lr': lr0, 'lrd': lrd})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
for i in range(num_steps):
loss = svi.step(predictors, hidden_feat, pheno)
if i % 1000 == 0:
print(loss)
predictive = Predictive(model, guide=guide, num_samples=1000,
return_sites=['g0', 'covs', 'pi', 'z'])
samples = predictive(predictors, hidden_feat, pheno)
np.mean(samples['covs'].numpy(), axis=0)
np.mean(samples['pi'].numpy(), axis=0)
np.mean(samples['z'].numpy(), axis=0)
I just want to be sure I am using this distribution correctly, both in the model and guide. If there are better ways to attack this toy problem, I am also open to them (and additional education on enumeration, which I am still working on understanding).
[1] Inference with Discrete Latent Variables — Pyro Tutorials 1.8.6 documentation
[2] Tensor shapes in Pyro — Pyro Tutorials 1.8.6 documentation
[3] Discrete Inference with TraceGraph_ELBO - #5 by nmancuso
[4] Distributions — Pyro documentation