Different results from SVI and MCMC

numpyro
1

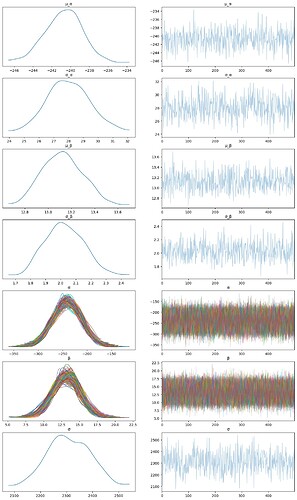
Hi all,

I try to run the bayesian hierarchical linear regression tutorial as Bayesian Hierarchical Linear Regression — NumPyro documentation and got the same results with tutorial.

But when I try to use SVI to solve the same problem, I got total different results. Did anything go wrong? Any suggestion will be useful.

Best !

Below is full codes for SVI

import torch
import pandas as pd
import numpy as np
from jax import random
from sklearn.preprocessing import LabelEncoder
import seaborn as sns
import matplotlib.pyplot as plt
import arviz as az

import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO, Predictive
from pyro.infer.autoguide import AutoDiagonalNormal

train = pd.read_csv(
    "https://gist.githubusercontent.com/ucals/"
    "2cf9d101992cb1b78c2cdd6e3bac6a4b/raw/"
    "43034c39052dcf97d4b894d2ec1bc3f90f3623d9/"
    "osic_pulmonary_fibrosis.csv"
)
train.head()
patient_encoder = LabelEncoder()
train["patient_code"] = patient_encoder.fit_transform(train["Patient"].values)

FVC_obs = train["FVC"].values
Weeks = train["Weeks"].values
patient_code = train["patient_code"].values

def model_pyro(patient_code, Weeks, FVC_obs=None):
    μ_α = pyro.sample("μ_α", dist.Normal(0.0, 500.0))
    σ_α = pyro.sample("σ_α", dist.HalfNormal(100.0))
    μ_β = pyro.sample("μ_β", dist.Normal(0.0, 3.0))
    σ_β = pyro.sample("σ_β", dist.HalfNormal(3.0))

    n_patients = len(np.unique(patient_code))

    with pyro.plate("plate_i", n_patients):
        α = pyro.sample("α", dist.Normal(μ_α, σ_α))
        β = pyro.sample("β", dist.Normal(μ_β, σ_β))

    σ = pyro.sample("σ", dist.HalfNormal(100.0))
    FVC_est = α[patient_code] + β[patient_code] * Weeks

    with pyro.plate("data", len(patient_code)):
        pyro.sample("obs", dist.Normal(FVC_est, σ), obs=FVC_obs)
guide = AutoDiagonalNormal(model_pyro)
adam = pyro.optim.Adam({"lr": 0.03})
svi = SVI(model_pyro, guide, adam, loss=Trace_ELBO())

patient_code = torch.tensor(patient_code)
FVC_obs = torch.tensor(FVC_obs)
Weeks = torch.tensor(Weeks)

pyro.clear_param_store()
for j in range(10000):
    # calculate the loss and take a gradient step
    loss = svi.step(patient_code, Weeks, FVC_obs=FVC_obs)

predictive = Predictive(model_pyro, guide=guide, num_samples=500)
preds = predictive(patient_code, Weeks)
sanitized_preds = {k: v.unsqueeze(0).detach().numpy() for k, v in preds.items() if k != 'obs'}

pyro_data = az.convert_to_inference_data(sanitized_preds)
az.plot_trace(pyro_data, compact=True,figsize=(15, 25))
2

here is the output of SVI, and you can see the results of MCMC at Bayesian Hierarchical Linear Regression — NumPyro documentation

svi
svi1182×1987 185 KB

3

I found the posterior distribution of sigma via MCMC obey Normal distribution, which seems not influenced by the prior distribution.

But in SVI, set the right posterior in guide() is important and difficult . So I choose Normal distribution (inspired by MCMC results ). But I found it may sample negative value for sigma

I find my problem is quite similar with Setting constraints and guides on constrained distributions.

Does this mean that svi is not applicable in hierarchical Bayesian ?

4

You might have some luck with AutoMultivariateNormal. Variables in hierarchical Bayesian are typically correlated; hence, a mean field variational distribution might not work.

5

it’s also unlikely that this is a good optimization scheme

adam = pyro.optim.Adam({“lr”: 0.03})

you need to drop the learning rate at least to some degree over the course of optimization. see #3 here and other tips

6

Thanks for your rely , I will reduce the learning rate and have a try

7

Thanks for your reply, this is may be the key point, could you consider provide a tutorial for using SVI in Hierachical Bayesian. This could be very helpful, since it is a important part in probablistic machine learning. Current tutorial uses the MCMC only, which is can not reflect the advantage of Pyro.