I’m comparing Pyro and NumPyro on a 1-layer (50 hidden dim) BNN with an AutoNormal guide and seeing substantially better results with Pyro on the UCI datasets with the standard splits from On the Importance of Strong Baselines in Bayesian Deep Learning. I see the same trend with all of the UCI regression benchmarks. If I use AutoDelta, the difference disappears, and the results are on par with the literature.
Does Pyro implement optimizations not in NumPyro that could explain the difference?
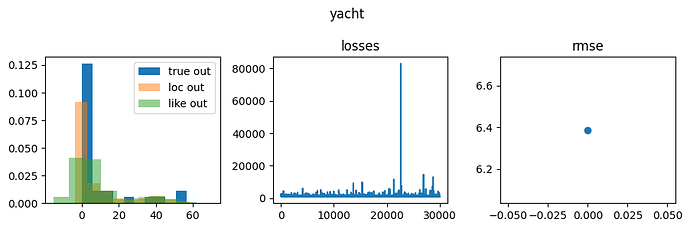
Pyro Yacht results
Like is short for likelihood and corresponds to samples from
sample site y, and loc corresponds to network outputs, i.e., deterministic site y_loc in the network below.
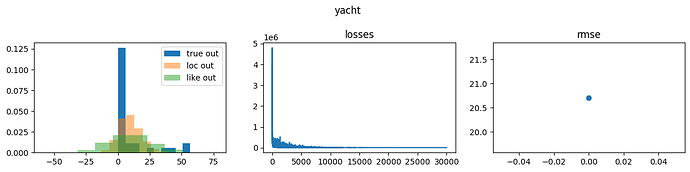
NumPyro Yacht results
Notice that the precision is lower, and the network locations are further from the ground truth with NumPyro than with Pyro. Both lead to poor performance; however, whether one is causal or the other is not clear.
Training
def train_svi(x, y):
with seed(rng_seed=0): # Change seed doesn't affect the difference
svi = SVI(model, AutoNormal(model), Adam(1e-3), Trace_ELBO())
res = svi.run(prng_key(), STEPS, x, y, subsample=100) # Pyro version uses step.
return svi, res
BNN
def bnn(x, y, subsample):
"""BNN described in Appendix D of [1]
**References:**
1. *UNDERSTANDING THE VARIANCE COLLAPSE OF SVGD IN HIGH DIMENSIONS*
Jimmy Ba, Murat A. Erdogdu, Marzyeh Ghassemi, Shengyang Sun, Taiji Suzuki, Denny Wu, Tianzong Zhang
"""
hdim = 50
prec = sample('prec', Gamma(2., 2.))
w1 = sample(
"nn_w1",
Normal(0.0, 1.0).expand((x.shape[1], hdim)).to_event(2)) # prior on l1 weights
b1 = sample("nn_b1", Normal(0.0, 1.0).expand((hdim,)).to_event(1)) # prior on output bias term
w2 = sample("nn_w2", Normal(0.0, 1.0).expand((hdim, hdim)).to_event(2)) # prior on l1 weights
b2 = sample("nn_b2", Normal(0.0, 1.0).expand((hdim,)).to_event(1)) # prior on output bias term
w3 = sample("nn_w3", Normal(0.0, 1.0).expand((hdim,)).to_event(1)) # prior on output weights
b3 = sample("nn_b3", Normal(0.0, 1.0)) # prior on output bias term
with plate(
"data",
x.shape[0], subsample_size=subsample if subsample is not None else x.shape[0]
) as idx:
x_batch = x[idx]
y_batch = y[idx] if y is not None else y
# 2 hidden layer with tanh activation
loc_y = deterministic(
"y_loc", nn.relu(nn.relu(x_batch @ w1 + b1) @ w2 + b2) @ w3 + b3
)
sample(
"y",
Normal(loc_y, jnp.sqrt(1/prec)),
obs=y_batch,
)