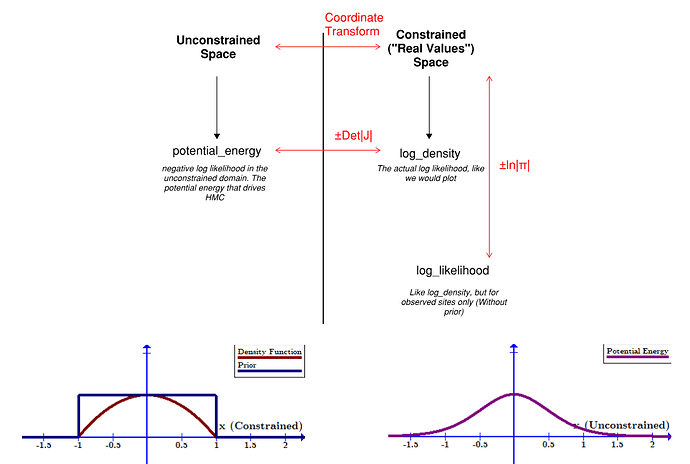
Note quite, because the probability density changes as you shift between coordinates. The core idea here is they are densities, and so equivalent differential elements need to have the same total power contained within them. E.g., if I have some constrained parameter x that converts to unconstrained parameter z, I need:
P_x(x) dx = P_z(z) dz
Which of course rearranges to:
P_x(x) \cdot\frac{dx}{dz} = P_z(z) \\
\ln \vert P_x(x) \vert + \ln \vert \frac{dx}{dz}\vert = \ln \vert P_z(z)\vert
I.e. to go between the two log-densities I need to add a log of the derivative.
If I have many parameters being transformed, like:
x_1 \rightarrow z_1(x_1) \\
x_2 \rightarrow z_2(x_2) \\
\vdots \\
I need to correct by the product of all of these:
\ln \vert P_z(z)\vert = \ln \vert P_x(x) \vert + \ln \vert \frac{dx_1}{dz_1} \frac{dx_2}{dz_2} \dots \vert
And in the more general case where the transformed parameters “mix”, i.e.:
x_1 \rightarrow z_1(x_1, x_2 \dots) \\
x_2 \rightarrow z_2(x_1, x_2 \dots) \\
\vdots \\
The correction factor is the determinant of the Jacobian of all of these transformations:
J = \left[ \matrix{{\frac{\partial z_1}{\partial x_1},\frac{\partial z_1}{\partial x_2}}\\{\frac{\partial z_2}{\partial x_1},\frac{\partial z_2}{\partial x_2}}} \right]
\ln \vert P_z(z)\vert = \ln \vert P_x(x) \vert + \ln \vert det(J) \vert
Throw in a negative or two to account for inverses and the difference between density and potential energy, and you have a clearer picture