Difference between simple ELBO and Trace_ELBO

Misc.
1

I’m trying to understand Pyro’s implementation, so I was studying MiniPyro (which has been super useful!). I’ll share a blog post with my experiences soon.

One specific issue I ran into is variational inference with discrete random variables. Specifically, I have a simple model:

def sleep_model():
    feeling_lazy = sample("feeling_lazy", dist.Bernoulli(0.9))
    if feeling_lazy:
        ignore_alarm = sample("ignore_alarm", dist.Bernoulli(0.8))
        amount_slept = sample("amount_slept", 
                              dist.Normal(8 + 2 * ignore_alarm, 1))
    else:
        amount_slept = sample("amount_slept", dist.Normal(7, 0.5))
    return amount_slept

And I wanted to do a basic analysis on the posterior when observing amount_slept.

def sleep_guide():
    lazy_prior = param("lazy_prior", tensor(0.9), constraint=constraints.interval(0., 1.))
    ignore_prior = param("ignore_prior", tensor(0.8), constraint=constraints.interval(0., 1.))
    feeling_lazy = sample("feeling_lazy", dist.Bernoulli(lazy_prior))
    if feeling_lazy:
        sample("ignore_alarm", dist.Bernoulli(ignore_prior))

cond_sleep_model = condition(sleep_model, {"amount_slept": 6.5})
optimizer = Adam({"lr": 0.01, "betas": (0.90, 0.999)})
svi = SVI(cond_sleep_model, sleep_guide, optimizer, loss=Trace_ELBO())

for _ in range(1000):
    svi.step()

This has the intended effect of lowering the priors:

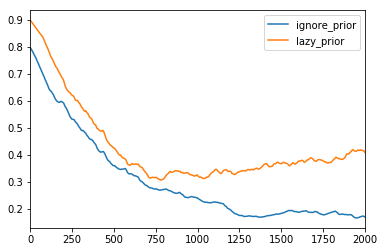
image

However, if I use the “simple” ELBO from tutorial:

def elbo_loss(model, guide):
    guide_trace = trace(guide).get_trace()
    model_trace = trace(replay(model, guide_trace)).get_trace()
    return -(model_trace.log_prob_sum() - guide_trace.log_prob_sum())
        
svi = SVI(cond_sleep_model, sleep_guide, optimizer, loss=elbo_loss)

This does not have the intended effect:

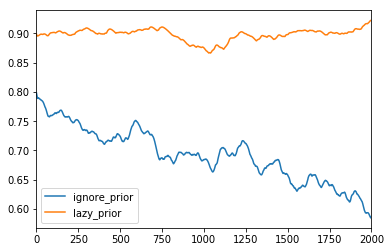
image

First, what is the theoretical reason for this issue? MiniPyro says this ELBO only supports “random variables with reparameterized samplers”. Does the Bernoulli distribution not have a reparameterized sampler? If so, are there good resources that explain the issue and why that is?

Second, what is the smallest change I could make to the elbo_loss function to work equivalently to Trace_ELBO in this specific instance? The actual Trace_ELBO source code is fairly complex so I’m trying to implement a more minimal example if possible.

1 Like
2 
def elbo_loss_improved(model, guide)
    guide_trace = trace(guide).get_trace()
    model_trace = trace(replay(model, guide_trace)).get_trace()
    model_prob = model_trace.log_prob_sum()
    guide_prob = guide_trace.log_prob_sum()
    elbo = model_prob - guide_prob  
    surrogate_elbo = elbo * (guide_prob + 1.) + guide_prob
    return -surrogate_elbo

For this specific problem, this adaptation/simplification of the Trace_ELBO code seems to work, but I certainly cannot explain why.

3

you might start by reading this

1 Like