Diagnosing convergence for a very simple model

numpyro
1

I’ve been trying to monitor convergence of model parameters using the cosine similarity between changes of parameter values. The basic idea is as follows. If the variational parameters are very far from the optimum, the optimizer will consistency push the parameters in the right direction and the similarity between changes is large. If the variational parameters are close to the optimum, updates are less consistent as we bounce around the optimum, and the cosine similarity is small.

More formally,

\begin{aligned} \delta_t &= \theta_t - \theta_{t - 1}\\ \rho_t &= \frac{\delta_t^\intercal \delta_{t-1}}{\left\Vert\delta_t\right\Vert\left\Vert\delta_{t-1}\right\Vert}, \end{aligned}

where \theta_t are the parameters at epoch t, \delta_t is the change from \theta_{t-1} to \theta_t after having run one epoch, and \rho_t is the cosine similarity between changes fro successive epochs.

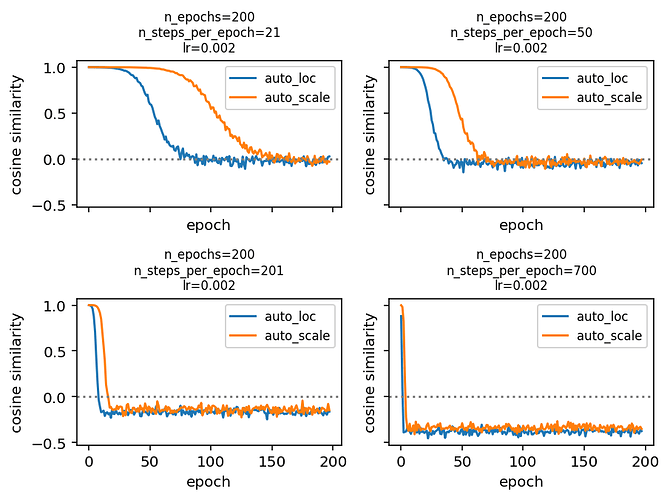
What I expected to see is that we start of with \rho_1\approx 1 and find \rho_t bouncing around 0 for large t. What I actually observe is that \rho_t becomes—and consistently stays—negative if the number of steps per epoch is large enough. Do you have any ideas what might be going on here?

I’ve created a reproducible example here for a simple model x\sim\mathsf{Normal}(0, 1) for x\in\mathbb{R}^{1,000}. The plot of cosine similarity against epoch number looks like this using an AutoDiagonalNormal guide.

similarity
similarity906×676 71.5 KB

A few hypotheses I’ve tested and ruled out:

  • Maybe the optimizer steps back and forth over the optimum with each iteration (not epoch) if the learning rate is too large. But I observe the same behavior for even and odd numbers of steps per epoch, so that’s probably not it.
  • Maybe it’s something to do with the optimizer, but I observe the same behavior for adam and sgd from the optax package.
  • Maybe I’ve picked the number of iterations per epoch “just right” so the parameters walk from one side to the other side of the optimum. But I observe the same behavior for different number of iterations per epoch.
  • Maybe it’s got something to do with dimensionality, but I observe the same behavior for x\in\mathbb{R}^{100}.

Any insights would be much appreciated! Pretty sure my logic is flawed somewhere. Thanks for your time.

1 Like
2

have you tried e.g. exponentially reducing the lr?

3

I think learning rate scheduling could help here. Having said that, I’m keen to get my head around exactly what’s happening because it feels like there’s something deeper (or more likely a bug in my code).

4

i can’t really say but i think with a fixed learning there can be a tendency to “bounce from one valley slope to the next” once you get close to the optimum so in that world you might imagine a negative cosine similarity, though perhaps i would expect something of smaller magnitude like -0.03

5

Yes, agreed regarding the bouncing from one side of the valley to the other. The reason I was surprised is that I measure the changes between epochs rather than between individual update steps. The negative correlation seems to hold independent of the number of iterations per epoch, provided that the number of iterations is large enough (e.g., as shown in the bottom two panels of the first post).