Dependency visualising [Bayesian Network]

1

I have a question on visualising dependency between r.v. in Pyro.
Is there an easy way I can plot the dependency graph of the variables? I am trying to work with Bayesian Networks, and sometimes they get too large and complex to understand using pyros plates, especially since Pyro assumes dependency between every r.v. and the previous one.

To check my understanding of Pyros plate, I am trying to model the following system:
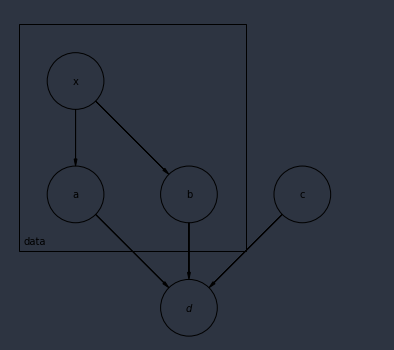
image

Is this model fine?

def model(data):
    x_prior_a = pyro.sample('x_prior_a', dist.Uniform(0, 1))
    # etc.. assume all numbers from now are just priors. Priors aren't dependent on each other
    with pyro.plate("high_level", 2):
        x = pyro.sample('x', dist.Beta(x_prior_a, 1))
        with pyro.plate("data", len(data)):
            a = pyro.sample('a', dist.Normal(10, 2))
            b = pyro.sample('b', dist.Beta(1, 1))
        c = pyro.sample('c', dist.Uniform(0, 10))
      d = pyro.sample('d', dist.Normal(a + b - C, 5), obs=true_function(data))
  return x,c,a,b,d

or should I be a lot more explicit with my plates?

def model2(data):
    x_prior_a = pyro.sample('x_prior_a', dist.Uniform(0, 1))
    # etc.. assume all numbers from now are just priors. Priors aren't dependent on each other
    with pyro.plate('c_plate', 1):
         c = pyro.sample('c', dist.Uniform(0, 10))
    data_plate =  pyro.plate('data', len(data), dim=-2)
    with data_plate:
      with pyro.plate('first_plate', 1):
        a = pyro.sample('a', dist.Normal(10, 2))
      with pyro.plate('second_plate', 1):
        b = pyro.sample('b', dist.Beta(1, 1))
      # d is still in data_plate context
      d = pyro.sample('d', dist.Normal(a + b - C, 5), obs=true_function(data))
  return x,c,a,b,d

Is there a way to disable automatic dependency in pyro?

Many thanks!

2

Is there an easy way I can plot the dependency graph of the variables?

I found that daft is helpful for plotting a Bayesian model. :smiley:

I found it tricky to detect the dependency of a variable X w.r.t. a variable Y. I guess you can condition X on some tensor value with requires_grad=True, and then check if the log_prob at Y has requires_grad=True or not.

In your plot, because d does not belong to data plate, I guess you can make the data dimension of a, b, x dependent dimensions (rather than independent dimensions) using dist.Normal(0, 1).expand([len(data)]).to_event() for example.

If d belongs to data plate, then you can model as follows

with pyro.plate("high_level", 2):
    c = pyro.sample('c', dist.Uniform(0, 10))
    with pyro.plate("data", len(data)):
        x = pyro.sample('x', dist.Beta(x_prior_a, 1))
        a = pyro.sample('a', dist.Normal(10, 2))
        b = pyro.sample('b', dist.Beta(1, 1))
        d = pyro.sample('d', dist.Normal(a + b - C, 5), obs=true_function(data))

In other words, your model should correspond 1-1 w.r.t. your plot.

1 Like
3

Thank you for your reply! It would be pretty neat if we can integrate daft with Pyro somehow to aid with debugging. Indeed d is dependent on the data I made a mistake in my plot :slight_smile:

Thanks for the code snippet, so should I always assume independence between variables under the same plate?
Like in the code are a and b independent? I might have misunderstood the docs if they are.
But then why did we need a high_level plate to indicate c and x are independent, but we didn’t need it for a and b?

My confusion arises from the following Pyro’s tutorial on shapes: Is it always safe to assume dependence and this thread: Dependency tracking in pyro

In the second thread, even though both a and b were under a plate, it was mentioned that they are dependent

  with pyro.plate("my_plate1", 2):
        a =  sample('a', Bernoulli(0.5))
        b = sample('b',  Bernoulli(0.5))

… rest of the thread:
a[0] and b[0] are in the same slice (0) and by the first rule above b[0] is assumed to depend on a[0].

4

Sorry, I thought that the high_level plate is an additional dimension that you need because your data has shape 2xN. If that is not the case, you should remove it.

In my last code, a and b are independent. However, there is no Pyro declaration that they are independent. Rather than that, it is infered (by human) from the context. If we are interested in the joint distribution of a and b, then p(a, b) = p(a) p(b|a) (which is equal to p(a) p(b)). Pyro will compute p(a) and p(b|a). Though Pyro does not know that a and b are independent, p(b|a) will be p(b) in your model. If, for example, b = Normal(a, 1), then p(b|a) will be different from p(b). They are also different when, as in your plate plot, a and b are dependent but they are independent conditioned on x.

Pyro code is corresponding 1-1 to plate notation. You should use 1 plate when your diagram has 1 plate. You can look at those examples which illustrate a variety of models and their corresponding 6 plate diagrams (in the reference).

1 Like
5

I see this is very helpful, the examples too! Thanks a lot for your time.

One last question (hopefully). So am I right to assume that Pyro samplers don’t make use of the independence to improve their efficiency?
like in this example, the joint distribution (from Pyro’s inference perspective) is actually: p(d,b,a,x,c) = p(d|b,a,x,c)p(b|a,x,c)p(a|x,c)p(x|c)p(c) which expands even further and there is no way to tell it to use this joint distribution instead: p(d,b,a,x,c) = p(d|a,b,c)p(a|x)p(b|x)p(c)?
Umm, this hinders the advantages of using Bayesian Network on Pyro then…

6

Yes, you might not tell Pyro should use the later formula. But the real computation will use the later formula (with an additional p(x|c) term, and the computation is performed from right to left). I found there is no disadvantage in computation here, unless you want Pyro to parallel sample or parallel compute probabilities at a and b (i.e. computing some quantities at a and b at the same time, given that they are independent conditioning on their father variables). Is that your usage case?

1 Like
7

Thanks a lot, really appreciate all the help.
My end use-case is modelling a large Bayesian network with 100 r.v.
The idea is to model the effect of parameters on a large system with limited data points.
Computation tractability is one reason yes, the other (and more important for my use case) is that I am worried about not being able to properly utilise conditional independence in the joint probability and exploit the decomposability resulting in the large bayesian network will require more samples than necessarily. Collecting these samples from the real system is very expensive and time consuming process.

I will continue with Pyro for now, I suppose if I face the issue down the road I will see how hard it is to get the inference engine to use independence knowledge.