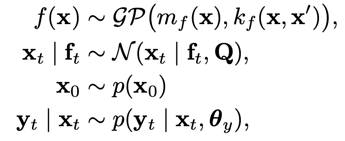Hi,
I am new to Pyro and I am trying to build a GPSSM using Pyro. GPSSM is presented below. Detailed model description can be found in this paper.
The following is my code snippet. I was wondering if this code is written in an appropriate way? Is that correct? Should I use pyro.sample() to specify the latent variable f (latent_gp)? The code now only works for the case of N = 1, which means that I can only sample 1 time series. What should I modify on the part of GP so that I can sample more time series (N>1)? Any advice and suggestions will be greatly appreciated, thank you.
# define model
def gp_ssm(data=None, N=1, T=2, d=1):
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(T,))
y = 0.5 * torch.sin(3 * X) + dist.Normal(0.0, 0.2).sample(sample_shape=(T,))
Xu = torch.arange(20.) / 4.0
# initialize the kernel and model
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=d)
# we increase the jitter for better numerical stability
# sgpr = gp.models.SparseGPRegression(X, y, kernel, Xu=Xu, noise=torch.tensor(0), jitter=1.0e-5)
sgpr = gp.models.GPRegression(X, y, kernel, noise=torch.tensor(0.))
# the latent time series you want to infer
# initialize a vector where you'll save the inferred values
latent = torch.empty((T, N))
latent_gp = torch.empty((T, N))
# Plate out the same state space model for N different obs
with pyro.plate('data_plate', N) as n:
x0 = pyro.sample('x0', dist.Normal(0, 1)) # or whatever your IC might be
latent[0, n] = x0
latent_gp[0, n] = x0
# Assume the transition noise is a white Gaussian
# The markov part
for t in pyro.markov(range(1, T)):
# for t in range(1, T):
if t == 1:
# generation of f1:
cov = torch.eye(1)
latent_gp[t, n] = dist.Normal(torch.zeros(t), cov). \
sample(sample_shape=(1,))
# generation of x1: 【Note: transition noise is a white Gaussian 】
x_t = pyro.sample(
f"x_{t}",
dist.Normal(latent_gp[t, n] + 0, torch.eye(1))
)
y_t = pyro.sample(
f"y_{t}",
dist.Normal(x_t, .1), # observation noise: N(x_t, 0.1)
obs=data[t - 1, n] if data is not None else None
)
latent[t, n] = x_t
else:
# generation of x2:
latent_gp_input = latent[0:t - 1, n].reshape(-1,)
latent_gp_temp = latent_gp[1:t, n].reshape(-1,)
# set training data
sgpr.set_data(latent_gp_input, latent_gp_temp)
# output the GP prediction
latent_gp[t, n], cov = sgpr(latent[t - 1, n], full_cov=True, noiseless=False)
# update state
x_t = pyro.sample(
f"x_{t}",
dist.MultivariateNormal(latent_gp[t, n] + 0, torch.eye(1))
)
y_t = pyro.sample(
f"y_{t}",
dist.Normal(x_t, .1), # observation noise: N(x_t, 0.1)
obs=data[t - 1, n] if data is not None else None
)
latent[t, n] = x_t
return pyro.deterministic('latent', latent)