I am trying to perform Bayesian neural network regression on a 1-D synthetic dataset, when defining the model, at first I used the known fixed noise level, everything goes fine, and then I defined a Gamma prior to the precision to see if I can get good posterior noise estimation, and then
-
The
Trace_ELBOloss value is much better than using fixed known precision -
The prediction and the quality of uncertainty get much worse
So I want to ask,
-
Why does a better ELBO gives much worse prediction?
-
What is a proper way to deal with unknown precision?
Below is my code, Bayesian neural network with fixed known precision:
import torch
import torch.nn as nn
import pyro
import pyro.optim
import numpy as np
from torch.distributions import constraints
noise_level = 0.01
num_data = 1000
xs = torch.linspace(-3, 3, num_data).reshape(num_data, 1)
ys = torch.FloatTensor(np.sinc(xs.numpy()))
ys = ys + noise_level * torch.randn_like(ys)
class BNN_SVI:
def __init__(self, dim, conf = dict()):
self.dim = dim
self.num_iters = conf.get('num_iters', 400)
self.print_every = conf.get('print_every', 100)
self.batch_size = conf.get('batch_size', 128)
self.lr = conf.get('lr', 1e-3)
self.weight_prior = conf.get('weight_prior', 1.0)
self.bias_prior = conf.get('bias_prior', 1.0)
self.prec_alpha = conf.get('prec_alpha', 3)
self.prec_beta = conf.get('prec_alpha', 1)
self.nn = nn.Sequential(
nn.Linear(self.dim, 50), nn.Tanh(),
nn.Linear(50, 1))
def model(self, X, y):
noise_scale = torch.tensor(noise_level)
# precision = pyro.sample("precision", pyro.distributions.Gamma(self.prec_alpha, self.prec_beta))
# noise_scale = 1 / precision.sqrt()
num_x = X.shape[0]
priors = dict()
for n, p in self.nn.named_parameters():
if "weight" in n:
priors[n] = pyro.distributions.Normal(
loc = torch.zeros_like(p),
scale = torch.ones_like(p)).to_event(1)
elif "bias" in n:
priors[n] = pyro.distributions.Normal(
loc = torch.zeros_like(p),
scale = torch.ones_like(p)).to_event(1)
lifted_module = pyro.random_module("module", self.nn, priors)
lifted_reg_model = lifted_module()
with pyro.plate("map", len(X), subsample_size = min(num_x, self.batch_size)) as ind:
prediction_mean = lifted_reg_model(X[ind]).squeeze(-1)
pyro.sample("obs",
pyro.distributions.Normal(prediction_mean, noise_scale),
obs = y[ind])
def guide(self, X, y):
softplus = nn.Softplus()
# alpha = pyro.param("alpha", torch.tensor(self.prec_alpha), constraint = constraints.positive)
# beta = pyro.param("beta", torch.tensor(self.prec_beta), constraint = constraints.positive)
# precision = pyro.sample("precision", pyro.distributions.Gamma(alpha, beta))
priors = dict()
for n, p in self.nn.named_parameters():
if "weight" in n:
loc = pyro.param("mu_" + n, self.weight_prior * torch.randn_like(p))
scale = pyro.param("sigma_" + n, softplus(torch.randn_like(p)), constraint = constraints.positive)
priors[n] = pyro.distributions.Normal(loc = loc, scale = scale).to_event(1)
elif "bias" in n:
loc = pyro.param("mu_" + n, self.bias_prior * torch.randn_like(p))
scale = pyro.param("sigma_" + n, softplus(torch.randn_like(p)), constraint = constraints.positive)
priors[n] = pyro.distributions.Normal(loc = loc, scale = scale).to_event(1)
lifted_module = pyro.random_module("module", self.nn, priors)
return lifted_module()
def train(self, X, y):
num_train = X.shape[0]
y = y.reshape(num_train)
self.x_mean = X.mean(dim = 0)
self.x_std = X.std(dim = 0)
self.y_mean = y.mean()
self.y_std = y.std()
self.X = (X - self.x_mean) / self.x_std
self.y = (y - self.y_mean) / self.y_std
optim = pyro.optim.Adam({"lr":self.lr})
svi = pyro.infer.SVI(self.model, self.guide, optim, loss = pyro.infer.Trace_ELBO())
pyro.clear_param_store()
self.rec = []
for i in range(self.num_iters):
loss = svi.step(self.X, self.y)
self.rec.append(loss / num_train)
if (i+1) % self.print_every == 0:
print("[Iteration %05d] loss: %.4f" % (i + 1, loss / num_train))
def sample(self):
net = self.guide(self.X, self.y)
return net
def sample_predict(self, nn, x):
return nn((x - self.x_mean) / self.x_std) * self.y_std + self.y_mean
conf = dict()
conf['num_iters'] = 5000
conf['batch_size'] = 32
conf['print_every'] = 50
conf['weight_priro'] = 1.
conf['bias_priro'] = 1.
conf['lr'] = 1e-1
conf['prec_alpha'] = 10. # precision mean = 20 variance = 40
conf['prec_beta'] = 0.5
model = BNN_SVI(dim = 1, conf = conf)
num_train = 20
train_id = torch.randperm(num_data)[:num_train]
train_x = xs[train_id]
train_y = ys[train_id]
model.train(train_x, train_y)
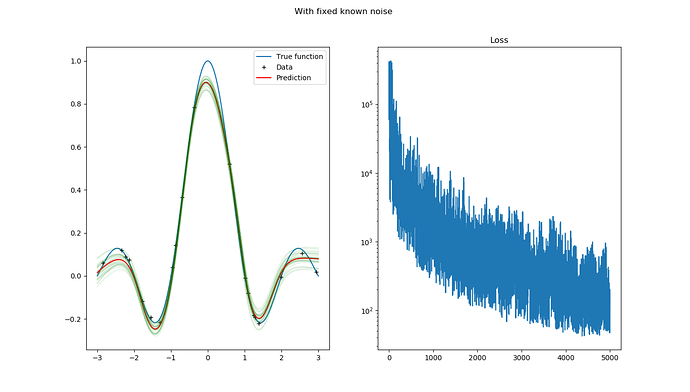
The prediction and the loss functions are plotted in the below figure, as can be seen, the prediction is pretty reasonable, while the final ELBO loss values are at the level of 1e2
However, if we replace noise_scale = torch.tensor(noise_level) in model function with
precision = pyro.sample("precision", pyro.distributions.Gamma(self.prec_alpha, self.prec_beta))
noise_scale = 1 / precision.sqrt()
And add corresponding parameter definition in guide function:
alpha = pyro.param("alpha", torch.tensor(self.prec_alpha), constraint = constraints.positive)
beta = pyro.param("beta", torch.tensor(self.prec_beta), constraint = constraints.positive)
precision = pyro.sample("precision", pyro.distributions.Gamma(alpha, beta))
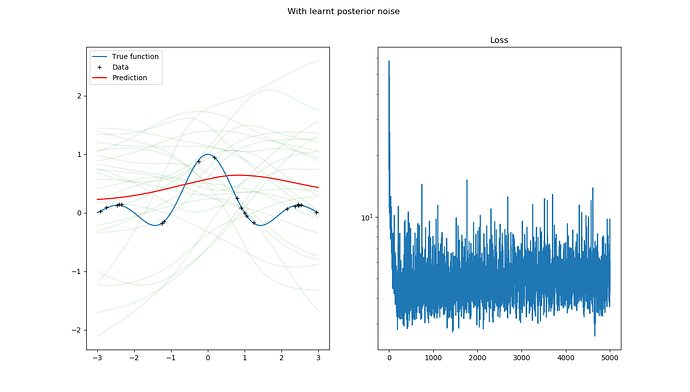
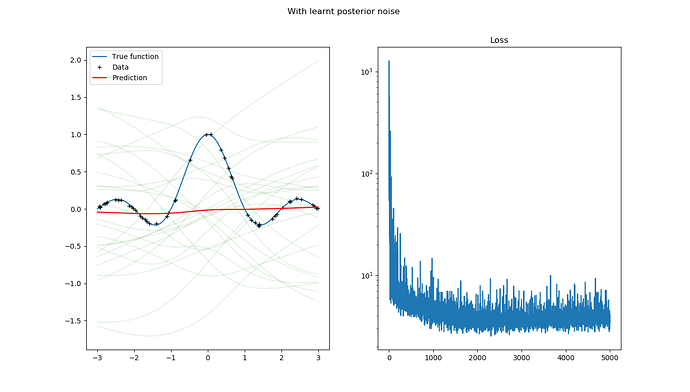
The prediction becomes this:
We can see that the ELBO loss goes below 10 very quickly.