Dataloaders with numpyro SVI?

[kjc7]

Are there any examples using standard pytorch dataloaders to train a numpyro svi model in batches?

In the example below, there are roughly 2.5 svi updates per second which is much slower than I’d hope.

losses = []
for epoch in tqdm(range(num_epochs)):
    epoch_loss = 0.
    for x,y in train_dataloader:
        svi_state, loss = svi.update(svi_state, X=x, y=y)
        epoch_loss += loss

    losses.append(epoch_loss)

Note: I have seen other examples that likely work much quicker like here, but I’m hoping to be able to use a torch dataloader, which is compatible with other model frameworks and allows me to keep the dataset structure upstream unchanged.

[kjc7]

Wanted to provide some reproducible code. here’s the main function, I got rid of the idea of epochs for now to make it more comparable with svi.run.

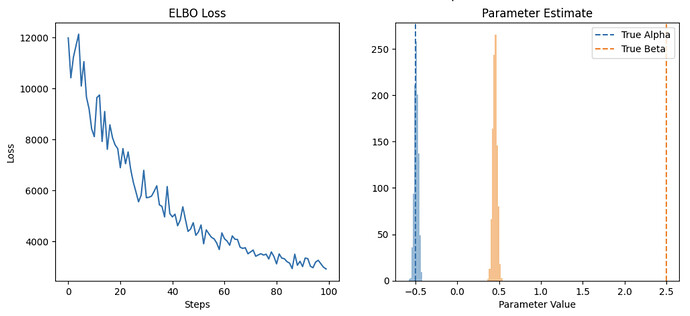
It takes a 10 seconds to fit on the data and it doesnt converge to the true parameter values after iterating through the full dataset, clearly I’m not thinking about this correctly. Is there a way to both speed this up and get it to converge to the true parameters after iterating through the full dataset?

def train_in_batches(model):
    SVIRunResult = namedtuple("SVIRunResult", ("params", "state", "losses"),)

    dataset= SimpleDataset(pd_dataset)
    data_loder = NumpyLoader(dataset, batch_size=1000, shuffle=True)

    # Define model fitting process
    optimizer = numpyro.optim.Adam(0.01)
    guide = AutoLowRankMultivariateNormal(model, init_loc_fn=numpyro.infer.init_to_median(), init_scale=0.025)
    svi = numpyro.infer.SVI(model, guide, optimizer, Trace_ELBO())

    # Set initial svi state
    sample_batch = next(iter(data_loder))
    svi_state = svi.init(PRNGKey(0), X=jnp.array(sample_batch[0]), y=jnp.array(sample_batch[1]))

    # Train
    losses = []
    for x,y in tqdm(data_loder):
        svi_state, loss = svi.update(svi_state, X=x, y=y)    
        losses.append(loss)

    svi_result = SVIRunResult(svi.get_params(svi_state), svi_state, losses)
    return svi_result, guide

Here’s the full code to reproduce

# ################
# Imports
# ################
from collections import namedtuple
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import default_collate

from jax import jit, lax, random
from jax.tree_util import tree_map
import jax.numpy as jnp
from jax.random import PRNGKey
from tqdm.notebook import tqdm

import numpyro
from numpyro import optim
import numpyro.distributions as dist
from numpyro.infer import SVI, Trace_ELBO
from numpyro.infer.autoguide import AutoLowRankMultivariateNormal

# ################
# Generate Data
# ################

SEED=99
np.random.seed(SEED)
N = 100000
beta = 2.5
alpha = -0.5
X = np.random.normal(0,1,size=N)
y = alpha + beta*X + np.random.normal(size=N)
pd_dataset = pd.DataFrame({"X":X, "y":y})

# ################
# Define Model
# ################

def model(X, y=None):
    beta = numpyro.sample("beta", dist.Normal(0,1))
    alpha = numpyro.sample("alpha", dist.Normal(0,1))
    sigma = numpyro.sample("sigma", dist.Exponential(1))

    mu = alpha + beta*X
    
    obs = numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)


# #################################
# Define training procedure 1
# #################################

def train_on_all_data(model):
    optimizer = numpyro.optim.Adam(0.01)
    guide = AutoLowRankMultivariateNormal(
        model, init_loc_fn=numpyro.infer.init_to_median(), init_scale=0.025
    )

    data = pd_dataset

    svi = numpyro.infer.SVI(model, guide, optimizer, Trace_ELBO())
    svi_result = svi.run(PRNGKey(0), 1000, X=data.X.values, y=data.y.values)
    return svi_result, guide


# #################################
# summarize training results
# #################################

def plot_results(svi_result, guide, method='svi.run'):
    fig, ax = plt.subplots(1,2, figsize=(12,5))
    
    ax[0].set(title="ELBO Loss",xlabel='Steps', ylabel='Loss')
    ax[0].plot( svi_result.losses )
    
    ax[1].set(title="Parameter Estimate",xlabel='Parameter Value')
    samples = guide.sample_posterior(PRNGKey(1), svi_result.params, (1000,))
    ax[1].hist( samples['alpha'], alpha=0.5 )
    ax[1].hist( samples['beta'], alpha=0.5 )
    ax[1].axvline(alpha, ls='--', label='True Alpha')
    ax[1].axvline(beta, ls='--', color='C1', label='True Beta')
    ax[1].legend()
    
    plt.suptitle(f"Fitted Model Results from {method}")


# #########################################################
# Create pytorch dataloader for training in batches
# #########################################################

class SimpleDataset(Dataset):
    def __init__(self, df, transform=None):
        self.df = df
    
    def __len__(self):
        return len(self.df)
    
    def __getitem__(self, idx):
        vals = self.df.iloc[[idx]].values
        X, target = vals[:,0], vals[:,1]
        return X,target
        
def numpy_collate(batch):
  return tree_map(np.asarray, default_collate(batch))

class NumpyLoader(DataLoader):
  def __init__(self, dataset, batch_size=1,
                shuffle=False, sampler=None,
                batch_sampler=None, num_workers=0,
                pin_memory=False, drop_last=False,
                timeout=0, worker_init_fn=None):
    super(self.__class__, self).__init__(dataset,
        batch_size=batch_size,
        shuffle=shuffle,
        sampler=sampler,
        batch_sampler=batch_sampler,
        num_workers=num_workers,
        collate_fn=numpy_collate,
        pin_memory=pin_memory,
        drop_last=drop_last,
        timeout=timeout,
        worker_init_fn=worker_init_fn)

# #########################################################
# Define training procedure for training in batches
# #########################################################

def train_in_batches(model):
    SVIRunResult = namedtuple("SVIRunResult", ("params", "state", "losses"),)

    dataset= SimpleDataset(pd_dataset)
    data_loder = NumpyLoader(dataset, batch_size=1000, shuffle=True)

    # Define model fitting process
    optimizer = numpyro.optim.Adam(0.01)
    guide = AutoLowRankMultivariateNormal(model, init_loc_fn=numpyro.infer.init_to_median(), init_scale=0.025)
    svi = numpyro.infer.SVI(model, guide, optimizer, Trace_ELBO())

    # Set initial svi state
    sample_batch = next(iter(data_loder))
    svi_state = svi.init(PRNGKey(0), X=jnp.array(sample_batch[0]), y=jnp.array(sample_batch[1]))

    # Train
    losses = []
    for x,y in tqdm(data_loder):
        svi_state, loss = svi.update(svi_state, X=x, y=y)    
        losses.append(loss)

    svi_result = SVIRunResult(svi.get_params(svi_state), svi_state, losses)
    return svi_result, guide


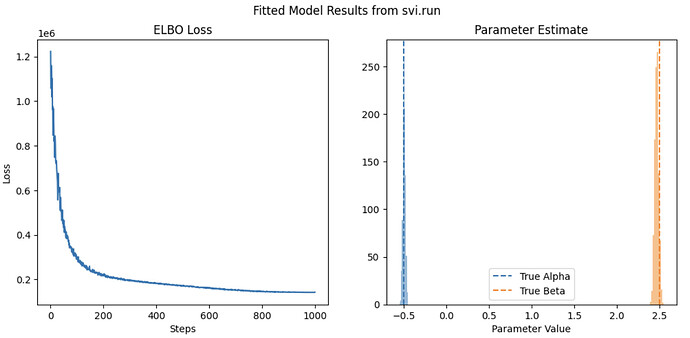
svi_result, guide = train_on_all_data(model)
plot_results(svi_result, guide)
plt.show()

svi_result_batched, guide_batched = train_in_batches(model)
plot_results(svi_result_batched, guide_batched, method='batched svi.update')
plt.show()

[martinjankowiak]

didn’t look at your code in detail but you probably need to use plate correctly so that the model knows how many total data points there are and thus how it should scale mini-batch contributions relative to global latent variables

[kjc7]

Thanks for calling that out. Any I updated that but it didnt improve parameter convergence or fit time for training in batches. I did decide to wrap the svi.update with jit and that sped things up a bit but didnt improve convergence. I’m guessing I’m just choosing a bad pattern, any more ideas?

Detailed the updated below

Update 1: Changed the model to use a plate for the observed data

def model(X, y=None):
    beta = numpyro.sample("beta", dist.Normal(0,1))
    alpha = numpyro.sample("alpha", dist.Normal(0,1))
    sigma = numpyro.sample("sigma", dist.Exponential(1))

    with numpyro.plate("n", X.shape[0]):
        mu = alpha + beta*X
        obs = numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)

I also attempted the following in case it helps to scale the likelihood more properly but I couldnt quite tell. Still couldnt get an improvement in parameter convergence

def model_subsample(X, y=None):
    total_dataset_size=100_000
    beta = numpyro.sample("beta", dist.Normal(0,1))
    alpha = numpyro.sample("alpha", dist.Normal(0,1))
    sigma = numpyro.sample("sigma", dist.Exponential(1))

    with numpyro.plate("n", total_dataset_size, subsample_size=X.shape[0]):
        mu = alpha + beta*X
        obs = numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)

Update 2: Incorprated JIT for the svi.update method

I copied the pattern from the jax guide here

def train_in_batches_jit(model):
    SVIRunResult = namedtuple("SVIRunResult", ("params", "state", "losses"),)

    dataset= SimpleDataset(pd_dataset)
    data_loader = NumpyLoader(dataset, batch_size=1000, shuffle=True)

    # Define model fitting process
    optimizer = numpyro.optim.Adam(0.01)
    guide = AutoLowRankMultivariateNormal(model, init_loc_fn=numpyro.infer.init_to_median(), init_scale=0.025)
    svi = numpyro.infer.SVI(model, guide, optimizer, Trace_ELBO())
    jit_update = jit(svi.update)

    # Set initial svi state
    sample_batch = next(iter(data_loader))
    svi_state = svi.init(PRNGKey(0), X=jnp.array(sample_batch[0]), y=jnp.array(sample_batch[1]))
    
    # Train
    losses = []
    for x,y in tqdm(data_loader):
        svi_state, loss = jit_update(svi_state, X=x, y=y)    
        losses.append(loss)

    svi_result = SVIRunResult(svi.get_params(svi_state), svi_state, losses)
    return svi_result, guide

[martinjankowiak]

model_subsample looks right. the plate needs to know both the total number of data points and the number of data points in the current batch.

i’d suggest demoting sigma to a parameter (and not a latent variable).

i would expect there may be limits to how well jax will optimize code that contains a pytorch dataloader. if you’re concerned about speed you should probably use a jax dataloader.

[kjc7]

Thanks for all of the feedback on this.

I realize now that the parameter convergence issue is just because I’m only performing an update 1 time for each batch in the dataset. In comparison, the train_on_all_data function which uses svi.run I think performs the update operation 1000 times on the entire dataset (since I specified 1000 training steps), as shown here

@martinjankowiak when you say a jax dataloader, what exactly are you referring to? In the jax docs they seem to imply that existing dataloaders such as pytorch should be used. I wonder if maybe I’m just not writing my code with the dataloader in a way thats efficient for jax?

Bringing this back to the big picture, I have a 5B entry dataset thats too large to handle the full thing in memory and load it into a numpyro model all at once. I’m trying to figure out the most efficient way to train it and load the data in properly. The code in this thread is just an extreme over-simplification of that. I’m also hoping as a result of this, I can start fitting PPL based models on massive datasets locally, which would be really amazing, but its not clear to me what the right workflow is for loading data in batches to numpyro.

I’ve seen the VAE example and maybe that is the answer here, but I find the existing data-loaders such as pytorch’s much easier to read and use and think they’d be better for a typical workflow

[martinjankowiak]

well when you’re training e.g. big neural networks any overhead from a dataloader is usually pretty small. but in you case each svi step is pretty fast so the dataloader overhead may be more important. i’m not saying you shouldn’t use pytorch dataloaders. that’s totally fine. i’m just saying that if you want to squeeze out every last millisecond you’d probably want a jax-native dataloader, perhaps something you’d have to implement from scratch